\[\newcommand{\u}[1]{\boldsymbol{\mathsf{#1}}} \renewcommand{\b}[1]{\boldsymbol{#1}} \newcommand{\t}[1]{\textsf{#1}} \newcommand{\m}[1]{\mathbb{#1}} \def\RR{\bf R} \def\bold#1{\bf #1} \def\mbf#1{\mathbf #1} \def\uv#1{\hat{\usf {#1}}} \def\dl#1{\underline{\underline{#1}}} \newcommand{\usf}[1]{\boldsymbol{\mathsf{#1}}} \def\bs#1{\usf #1}\]

Non-dimensional rigid body kinematics

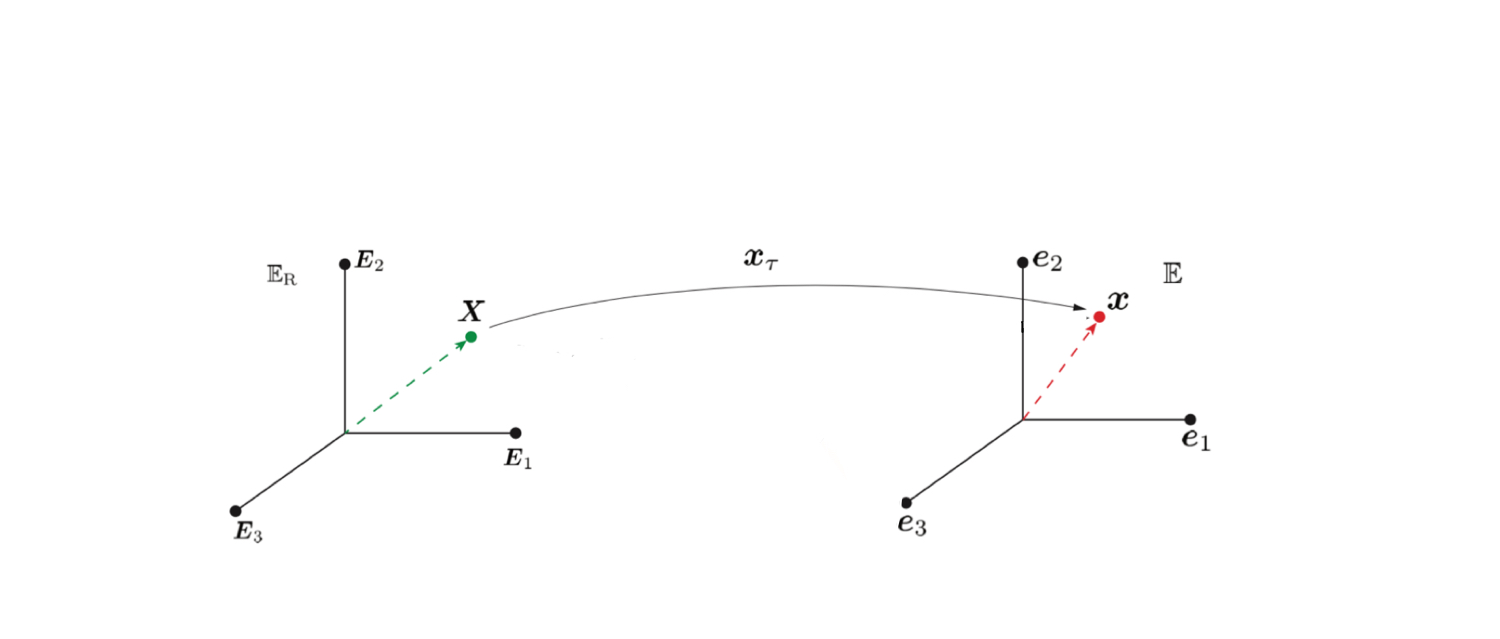
We discussed in class that the most general rigid body motion can be expressed as

\[\begin{align} \bs{x}_{\bs{t}}(\bs{X})&=\bs{R}(\bs{t})\bs{X}+\bs{c}(\bs{t}) \end{align}\]

The quantity $\bs{x}_{\bs{t}}(\bs{X})$ is the position vector in the space $\mathbb{E}$ at the time instance $\bs{t}$ of the particle that in the reference space $\mathbb{E}_{\rm R}$ had the position vector $\bs{X}$.

The quantity $\bs{R}(\bs{t})$ is the rotation linear operator that maps vectors from $\mathbb{E}_{\rm R}$ to vectors in $\mathbb{E}$. It does so keeping their length constant. The quantity $\bs{c}(\bs{t})$ is a vector in $\mathbb{E}$ that depends on time $\bs{t}$. It can be written as $c_{i}(\tau)\bs{e}_i$, where $(\bs{e}_{i})_{i\in (1,2,3)}$ is the set of basis vectors of $\mathbb{E}$.

The above motion in can be written using non-dimensional variables as

\[\begin{equation} \bs{x}_{\tau}(\bs{X})=\bs{R}(\tau)\bs{X}+\bs{c}(\tau) \label{eq:Motion} \tag{eq:Motion} \end{equation}\]

The quantity $\bs{x}_{\tau}(\bs{X})$ is the non-dimensional position vector at the non-dimensional time instance $\tau$ of the particle that in the reference space had the non-dimensional position vector $\bs{X}$. From here on we will be dropping the qualifier “non-dimensional,” since it will be clear from context whether we are talking about dimensional or non-dimensional quantities. We also use different fonts to denote dimensional and non-dimensional quantities. For an elaboration on this aspect see this section.

The quantity $\bs{R}(\tau)$ is an element of $SO(3)$, the special orthonormal group. It depends on time, as indicated by the presence of the non-dimensional time $\tau$ in it. The quantity $\bs{c}(\tau)=(c_{i}(\tau))_{i\in(1,2,3)}$. The quantity $\bs{X}$ is the non-dimensional position of the material particle $\mathcal{X}$ in the reference space $\mathbb{E}_{\rm R}$. It is discussed in detail in this section.

It follows from $\eqref{eq:Motion}$ that

\[\begin{align} \bs{V}_{\tau}(\bs{X})&=\bs{R}'(\tau)\bs{X}+\bs{c}'(\tau),\\ \bs{A}_{\tau}(\bs{X})&=\bs{R}''(\tau)\bs{X}+\bs{c}''(\tau).\\ \end{align}\]

The quantity $\bs{V}_{\tau}(\bs{X})$ is the non-dimensional velocity vector at the non-dimensional time instance $\tau$ of the particle that in the reference space had the non-dimensional position vector $\bs{X}$. Similarly, the quantity $\bs{A}_{\tau}(\bs{X})$ is the non-dimensional acceleration vector at the non-dimensional time instance $\tau$ of the particle that in the reference space had the non-dimensional position vector $\bs{X}$.

[edit]