\[\newcommand{\u}[1]{\boldsymbol{\mathsf{#1}}} \renewcommand{\b}[1]{\boldsymbol{#1}} \newcommand{\t}[1]{\textsf{#1}} \newcommand{\m}[1]{\mathbb{#1}} \def\RR{\bf R} \def\bold#1{\bf #1} \def\mbf#1{\mathbf #1} \def\uv#1{\hat{\usf {#1}}} \def\dl#1{\underline{\underline{#1}}} \newcommand{\usf}[1]{\boldsymbol{\mathsf{#1}}} \def\bs#1{\usf #1}\]

Rotations as Proper Orthogonal Transformations in \(\m{SO}(3)\)

Mathematica note is available here.

(i) \(\u{R}^{\t{T}} = \u{R}^{\t{-1}}\)

Proof:

The inverse transformation for a rotation \(\u{R}\, \sim\, (\theta, \u{e})\) clearly \(\u{R}^{-1} \, \sim\, (-\theta, \u{e})\). In invariant tensor notation, it is

\[\begin{align} \u{R}^{-1} &= \u{a}\otimes\u{a} + (\u{I}-\u{a}\otimes\u{a})\cos(-\theta) + (*\u{a})\sin(-\theta) \\ &= \u{a}\otimes\u{a} + (\u{I}-\u{a}\otimes\u{a})\cos(\theta) - (*\u{a})\sin(\theta) \end{align}\]

Recall from the previous section that the above formula for \(\u{R}^{-1}\) matches the formula for \(\u{R}^{\t{T}}\). Hence, \(\u{R}^{-1} = \u{R}^{\t{T}}\).

(ii) \(\t{det}(\u{R}) = +1\)

Proof:

Recall the formula,

\[\begin{align} \t{det}(\u{R}) = \frac{\u{R}\u{c}\cdot(\u{R}\u{a}\times\u{R}\u{b})}{\u{c}\cdot(\u{a}\times\u{b})} \end{align}\]

Choose without loss of generality that \(\left\{\u{a}, \u{b}, \u{c} \right\}\) are a right handed set of orthonormal vectors; \(\u{a}\times\u{b} = \u{c}\), and \(\u{a}\cdot\u{b} = \u{b}\cdot\u{c} = \u{c}\cdot\u{a} = 0\), and \(\left\|\u{a}\right\| =\left\|\u{b}\right\|=\left\|\u{c}\right\| = 1\).

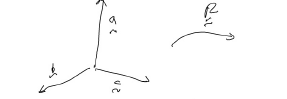
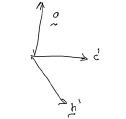
Since \(\u{a}, \u{b}, \u{c}\) are an orthonormal set of vectors,

\[\begin{align} \t{det}(\u{R}) &= \frac{(\u{R}\u{a})\cdot(\u{R}\u{b}\times\u{R}\u{c})}{\u{a}\cdot(\u{b}\times\u{c}) \: \Rightarrow 1 } \\ \t{det}(\u{R}) &= \u{a}\cdot(\u{R}\u{b}\times\u{R}\u{c}) \end{align}\]

Since \(\u{R}\u{b}\times\u{R}\u{c}\) will be a vector that has the magnitude \(\left\|\u{R}\u{b}\right\|\left\|\u{R}\u{c}\right\|\) and \(\perp\) to the plane spanned by \(\u{R}\u{b}\) and \(\u{R}\u{c}\). However, since \(\u{b}\) and \(\u{c}\) lie in a plane \(\perp\) to the axis of \(\u{R}\), \(\u{R}\u{b}\) and \(\u{R}\u{c}\) will again lie in the plane \(\perp\) to the axis of \(\u{R}\). Hence, the plane spanned by \(\u{R}\u{b}\) and \(\u{R}\u{c}\) is the plane spanned by \(\u{b}\) and \(\u{c}\), so the direction \(\perp\) to this plane is \(\u{a}\).

\[\begin{align} \u{R}\u{b}\times\u{R}\u{c} &= \left\|\u{R}\u{b}\right\|\left\|\u{R}\u{c}\right\|\u{a} \\ &= \left\|\u{b}\right\|\left\|\u{c}\right\|\u{a} \\ &= \u{a} \end{align}\] \[\begin{align} \boxed{\t{det}(\u{R}) = \u{a}\cdot\u{a} = 1} \end{align}\]

It follows from (i) and (ii) that \(\u{R}\in\m{SO}(N)\).

A technique to identify a Rotation:

A converse of the above result is also true. That is, if \(\u{R}\in\m{SO}(N)\) then \(\u{A}\) is a rotation transformation.

This result provides a unique characterization of rotation tensors. In checking whether a tensor represents a rotation, it is enough to check if the determinant is positive and if the transpose coincide with the inverse.

In summary:

\[\boxed{\u{R}\,\textrm{is a rotation}\, \Leftrightarrow{\u{R} \in \m{SO}(3)}}\]

[edit]