\[\newcommand{\u}[1]{\boldsymbol{\mathsf{#1}}} \renewcommand{\b}[1]{\boldsymbol{#1}} \newcommand{\t}[1]{\textsf{#1}} \newcommand{\m}[1]{\mathbb{#1}} \def\RR{\bf R} \def\bold#1{\bf #1} \def\mbf#1{\mathbf #1} \def\uv#1{\hat{\usf {#1}}} \def\dl#1{\underline{\underline{#1}}} \newcommand{\usf}[1]{\boldsymbol{\mathsf{#1}}} \def\bs#1{\usf #1}\]

Tensors: Components and Matrix Form

We have seen that vectors can be represented as column matrices. Today, we will see that tensors can be represented as square matrices. As before, let \(\{\hat{\bs{E}}_i\}_{i=1,2,3, \ldots, N}\) be a Cartesian set of basis vector that span \(\mathbb{E}^N\), where \(N\) is a positive integer. Typically, in enegineering mechanics problems, \(N=3\) or \(2\). Let \(\bs{a}\in \mathbb{E}^N\), and when \(N=3\) we have

\[\begin{align} \bs{a} &=a_1\hat{\bs{E}}_1+a_2\hat{\bs{E}}_2+a_3\hat{\bs{E}}_3\\ &=a_i \hat{\bs{E}}_i. \end{align}\]

Then the matrix representation of \(\bs{a}\) is,

\[\begin{equation} \left[\bs{a}\right]= \left[ \begin{array}{c} a_1\\ a_2\\ a_3\\ \end{array} \right] \end{equation}\]

Let \(\bs{T}\) be a tensor. That is, it is a linear mapping from \(\mathbb{E}^3\) to \(\mathbb{E}^3\). We define the matrix representation of \(\bs{T}\) as the \(3\times 3\) matrix that we denote as \(\left[ \bs{T}\right]\) that satisfies the following equation

\[\begin{align} \left[ \bs{T}\right] \left[ \bs{a}\right]&=\left[ \bs{T}\bs{a}\right] \end{align}\]

for all \(\bs{a}\in \mathbb{E}^3\).

Let \(\bs{T}\bs{a}=\bs{b}\), where

\[\begin{align} \bs{b} &=b_1\hat{\bs{E}}_1+b_2\hat{\bs{E}}_2+b_3\hat{\bs{E}}_3\\ &=b_i \hat{\bs{E}}_i, \end{align}\]

i.e., the matrix representation of \(\bs{b}\) is,

\[\begin{equation} \left[\bs{b}\right]= \left[ \begin{array}{c} b_1\\ b_2\\ b_3\\ \end{array} \right] \end{equation}\]

Then we have that,

\[\begin{align} \left[ \bs{T}\right] \left[ \bs{a}\right]&=\left[ \bs{b}\right]\\ \end{align}\]

Let \(T_{ij}\) be the \(i-j^{\text{th}}\) component of the matrix \(\left[\bs{T}\right]\), i.e., \(T_{ij}=\left[\bs{T}\right]_{ij}\). More explicitly,

\[\begin{align} \left[\bs{T}\right]&= \left[ \begin{array}{ccc} T_{11} && T_{12} && T_{13} \\ T_{21} && T_{22} && T_{23} \\ T_{31} && T_{32} && T_{33} \\ \end{array} \right] \end{align}\] \[\begin{align} \left[ \begin{array}{ccc} T_{11} && T_{12} && T_{13} \\ T_{21} && T_{22} && T_{23} \\ T_{31} && T_{32} && T_{33} \\ \end{array} \right] \left[ \begin{array}{c} a_1\\ a_2\\ a_3\\ \end{array} \right] &= \left[ \begin{array}{c} b_1\\ b_2\\ b_3\\ \end{array} \right] \end{align}\]

or equivalently,

\[\begin{align} T_{11}a_1 + T_{12}a_2 + T_{13}a_3 = b_1\\ T_{21}a_1 + T_{22}a_2 + T_{23}a_3 = b_2\\ T_{31}a_1 + T_{32}a_2 + T_{33}a_3 = b_3\\ \end{align}\]

Computing the matrix representation of a tensor

Motivating example

Let \(\bs{T}\) be a tensor that transforms the specific vectors \(\bs{a}\) and \(\bs{b}\) as follows:

\[\begin{align} \bs{T}\bs{a} = \bs{a} + 2\bs{b}, \bs{T}\bs{a} = \bs{a} - \bs{b}. \end{align}\]

Given a vector \(\bs{c} = 2\bs{a} + \bs{b}\), find \(\bs{T}\bs{c}\).

Solution

Using the linearity property of tensors, we have \(\begin{align} \bs{T}\bs{c} = \bs{T}(2\bs{a} + \bs{b})=2\bs{T}\bs{a} + \bs{T}\bs{b} = 2(\bs{a} + 2\bs{b}) + (\bs{a} - \bs{b}) = 3\bs{a} + 3\bs{b}. \end{align}\)

---

So let us start by defining the Matrix

\[\begin{align} \left[Q\right] &= \left[ \begin{array}{ccc} Q_{11} && Q_{12} && Q_{13} \\ Q_{21} && Q_{22} && Q_{23} \\ Q_{31} && Q_{32} && Q_{33} \end{array} \right] \end{align}\] \[\begin{align} \bs{T}\hat{\bs{E}}_1&=Q_{11}\hat{\bs{E}}_1+Q_{21}\hat{\bs{E}}_2+Q_{31}\hat{\bs{E}}_3\\ \bs{T}\hat{\bs{E}}_2&=Q_{12}\hat{\bs{E}}_1+Q_{22}\hat{\bs{E}}_2+Q_{32}\hat{\bs{E}}_3\\ \bs{T}\hat{\bs{E}}_3&=Q_{13}\hat{\bs{E}}_1+Q_{23}\hat{\bs{E}}_2+Q_{33}\hat{\bs{E}}_3\\ \end{align}\] \[\begin{align} \bs{T}\bs{a}&=\bs{T}\left(a_1\hat{\bs{E}}_1+a_2\hat{\bs{E}}_2+a_3\hat{\bs{E}}_3\right)\\ &=\bs{T}\left(a_1\hat{\bs{E}}_1\right)+\bs{T}\left(a_2\hat{\bs{E}}_2\right)+\bs{T}\left(a_3\hat{\bs{E}}_3\right)\\ &=a_1\left(\bs{T}\hat{\bs{E}}_1\right)+a_2 \left(\bs{T}\hat{\bs{E}}_2\right)+a_3\left(\bs{T}\hat{\bs{E}}_3\right)\\ \end{align}\] \[\begin{align} \bs{T}\bs{a} &=a_1\left(\bs{T}\hat{\bs{E}}_1\right)+a_2 \left(\bs{T}\hat{\bs{E}}_2\right)+a_3\left(\bs{T}\hat{\bs{E}}_3\right)\\ &=a_1\left(Q_{11}\hat{\bs{E}}_1+Q_{21}\hat{\bs{E}}_2+Q_{31}\hat{\bs{E}}_3\right)+a_2 \left(Q_{12}\hat{\bs{E}}_1+Q_{22}\hat{\bs{E}}_2+Q_{32}\hat{\bs{E}}_3\right)+a_3\left(Q_{13}\hat{\bs{E}}_1+Q_{23}\hat{\bs{E}}_2+Q_{33}\hat{\bs{E}}_3\right) \end{align}\] \[\begin{align} \bs{T}\bs{a} &=\left(Q_{11}a_1\hat{\bs{E}}_1+Q_{21}a_1\hat{\bs{E}}_2+Q_{31}a_1\hat{\bs{E}}_3\right)+ \left(Q_{12}a_2\hat{\bs{E}}_1+Q_{22}a_2\hat{\bs{E}}_2+Q_{32}a_2\hat{\bs{E}}_3\right)+\left(Q_{13}a_3\hat{\bs{E}}_1+Q_{23}a_3\hat{\bs{E}}_2+Q_{33}a_3\hat{\bs{E}}_3\right) \\ &= \left( Q_{11}a_1+ Q_{12}a_2+ Q_{13}a_3\right)\hat{\bs{E}}_1 + \left( Q_{21}a_1+ Q_{22}a_2+ Q_{23}a_3\right)\hat{\bs{E}}_2 + \left( Q_{31}a_1+ Q_{32}a_2+ Q_{33}a_3 \right)\hat{\bs{E}}_3 \end{align}\] \[\begin{align} \left[\bs{T}\bs{a}\right] &= \left[ \begin{array}{c} Q_{11}a_1+Q_{12}a_2+Q_{13}a_3\\ Q_{21}a_1+Q_{22}a_2+Q_{23}a_3\\ Q_{31}a_1+Q_{32}a_2+Q_{33}a_3 \end{array} \right] \\ \left[\bs{b}\right]&= \left[ \begin{array}{ccc} Q_{11} && Q_{12} && Q_{13} \\ Q_{21} && Q_{22} && Q_{23} \\ Q_{31} && Q_{32} && Q_{33} \end{array} \right] \left[ \begin{array}{c} a_1\\ a_2\\ a_3 \end{array} \right] \\ \left[ \begin{array}{c} b_1\\ b_2\\ b_3\\ \end{array} \right]&= \left[ \begin{array}{ccc} Q_{11} && Q_{12} && Q_{13} \\ Q_{21} && Q_{22} && Q_{23} \\ Q_{31} && Q_{32} && Q_{33} \end{array} \right] \left[ \begin{array}{c} a_1\\ a_2\\ a_3 \end{array} \right] \end{align}\]

which proves That

\[\begin{equation} \left[ \bs{T} \right]= \left[Q\right] \end{equation}\]

Example

Obtain the matrix for the tensor \(\bs{T}\) that transforms the base vectors as follows:

\[\begin{align} \bs{T}\bs{e}_1 &= 4\bs{e}_1 + \bs{e}_2, \\ \bs{T}\bs{e}_2 &= 2\bs{e}_1 + 3\bs{e}_3, \\ \bs{T}\bs{e}_3 &= -\bs{e}_1 + 3\bs{e}_2 + \bs{e}_3, \end{align}\]

Solution By the definition above,

\[\begin{align} \left[\bs{T}\right] &= \left[ \begin{array}{ccc} 4 && 2 && -1 \\ 1 && 0 && 3 \\ 0 && 3 && 1 \end{array} \right] \end{align}\]

---

Example

Obtain the matrix for the tensor \bs{T} that transforms the base vectors as follows:

\[\begin{align} \bs{T}\bs{e}_1 &= \bs{e}_1 + 2\bs{e}_2 + 3\bs{e}_3, \\ \bs{T}\bs{e}_2 &= 4\bs{e}_1 + 5\bs{e}_2 + 6\bs{e}_3, \\ \bs{T}\bs{e}_3 &= 7\bs{e}_1 + 8\bs{e}_2 + 9\bs{e}_3. \end{align}\]

Solution By inspection,

\[\begin{align} \left[\bs{T}\right] &= \left[ \begin{array}{ccc} 1 && 2 && 3 \\ 4 && 5 && 6 \\ 7 && 8 && 9 \end{array} \right] \end{align}\]

This example emphasizes again the convention we use to write the matrix of a tensor: The component of \(\bs{T}\bs{e}_{1}\) fills the first column, the component of \(\bs{T}\bs{e}_{2}\) fills the second column, and so on. The reason for this choice of convention will become obvious in the next section.

---

Example: Reflection across a plane

Let \(\bs{T}\) transform every vector into its mirror image with respect to a fixed plane; if \(\bs{e}_1\) is normal to the reflection plane (\(\bs{e}_{2}\) and \(\bs{e}_{3}\) are parallel to this plane), find a matrix of \(\bs{T}\).

Solution Because the normal to the reflection plane is transformed into its negative, and vectors parallel to the place are not altered, we have

\[\begin{align} \bs{T}\bs{e}_1 = -\bs{e}_1, \bs{T}\bs{e}_2 = \bs{e}_2, \bs{T}\bs{e}_3 = \bs{e}_3 \end{align}\]

which corresponds to

\[\begin{align} \left[\bs{T}\right] &= \left[ \begin{array}{ccc} -1 && 0 && 0 \\ 0 && 1 && 0 \\ 0 && 0 && 1 \end{array} \right]_{\bs{e}_i}. \end{align}\]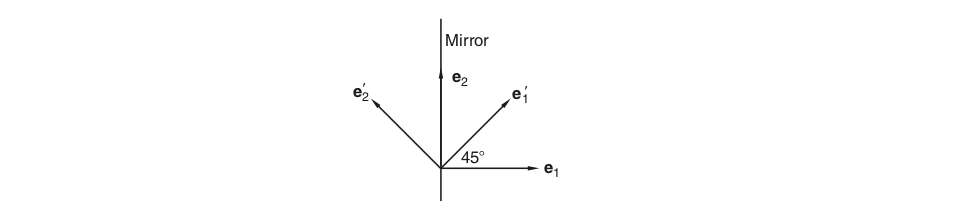

---

Example: 2D Rotation

Let \(\bs{R}\) correspond to a right-hand rotation of a rigid body about the \(x_3\)-axis by an angle \(\theta\). Find a matrix of \(\bs{R}\).

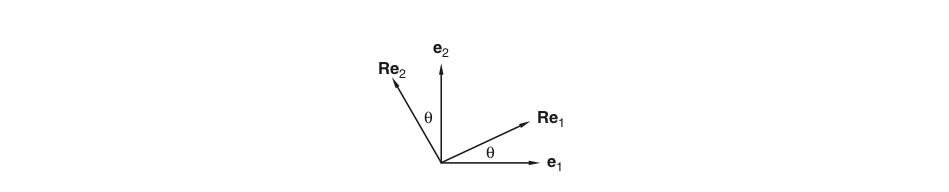
Solution From the figure, it is clear that

\[\begin{align} \bs{R}\bs{e}_1 &= \cos\theta\bs{e}_1 + \sin\theta\bs{e}_2, \\ \bs{R}\bs{e}_2 &= -\sin\theta\bs{e}_1 + \cos\theta\bs{e}_2, \\ \bs{R}\bs{e}_3 &= \bs{e}_3. \end{align}\]

which corresponds to

\[\begin{align} \left[\bs{R}\right] &= \left[ \begin{array}{ccc} \cos\theta && \sin\theta && 0 \\ \sin\theta && \cos\theta && 0 \\ 0 && 0 && 1 \end{array} \right]_{\bs{e}_i}. \end{align}\]

---

Example: Stretching Write the tensor \(\bs{T}\), defined by the equation \(\bs{T}\bs{a} = \alpha\bs{a}\), where \(\alpha\) is a constant and \(\bs{a}\) is arbitrary, in terms of the identity tensor, and find its components.

Solution Using the identity tensor, we can write \(\alpha\bs{a}\) as \(\alpha\bs{I}\bs{a}\), so that

\[\begin{align} \bs{T}\bs{a} = \alpha\bs{a} = \alpha\bs{I}\bs{a}. \end{align}\]

Since \(\bs{a}\) is arbitrary, therefore,

\[\begin{align} \bs{T} = \alpha\bs{I} \end{align}\]

The components of this tensor are clearly \(T_{ij} = \alpha\delta_{ij}\).

[edit]