\(\renewcommand{\u}[1]{\boldsymbol{#1}} \newcommand{\usf}[1]{\mathsf{\u{\mathsf{#1}}}} \newcommand{\lurd}[3]{^#1\!\!#2_{#3}} \newcommand{\lu}[2]{^#1\!\!#2} \newcommand{\pr}[1]{\left(#1\right)}\) ˛˛ 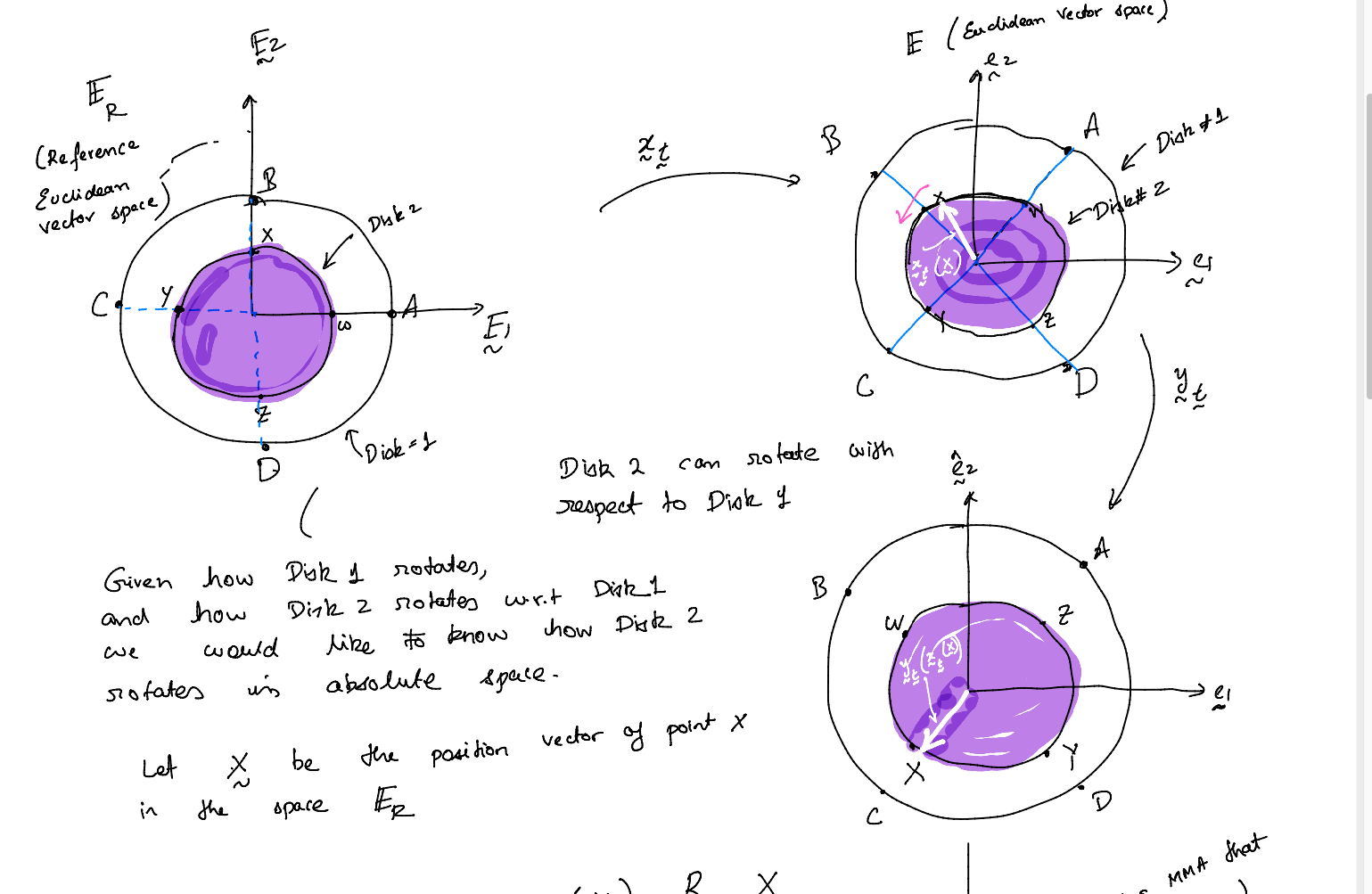The motion of (white) Disk #1 is given as

\[\begin{equation} \u{x}_{\u{t}}(\u{X})=\u{R}_{\u{t}} \u{X}+\u{c}(\u{t}) \label{eq:Motion} \tag{eq:Motion} \end{equation}\]

Column 1	Column 2	Column 3
$\u{c}(\u{t})$	$c_i(\tau)\u{e}_i$	Text
$\u{X}$	$X_i\u{E}_i$	Text
$\u{R}_{\u{t}}$	$R_{ij}(\tau)\u{e}_i\otimes \u{E}_j$	Text
$\u{x}_{\u{t}}(\u{X})$	$x_{i}(\usf{X},\tau)$, or $x_{i}(X_{*},\tau)$

We make some of the ensuing calculations appear less cumbersome let’s take $\mathcal{E}_{\rm ref}$ and $\mathcal{E}$ to be one and the same space, instead of two distinct compies of the Euclidean point space. This can be done by setting $\u{E}_i=\u{e}_i$ and $O=o$. The component representation of the different terms in $\eqref{eq:Motion}$ now reads

Column 1	Column 2	Column 3
$\u{c}(\u{t})$	$c_i(\tau)\u{e}_i$	Text
$\u{X}$	$X_i\u{e}_i$	Text
$\lurd{1}{\u{R}}{\u{t}}$	$\lurd{1}{R}{ij}(\tau)\u{e}_i\otimes \u{e}_j$	Text
$\u{x}_{\u{t}}(\u{X})$	$x_{i}(\usf{X},\tau)\u{e}_i$, or $x_{i}(X_{*},\tau)\u{e}_i$

On identidying $\mathcal{E}_{\rm ref}$ with $\mathcal{E}$ the reference configuration become’s rigid body $\mathcal{B}$’s initial configuration. Let $^1\mathcal{X}$ be particle belonging to Disk 1. If it is initially ($\u{t}=\u{o}$) located at $o+^1\u{X}$ then at the time instance $\u{t}$ it is located at point $o+\u{x}_{\u{t}}\left(^1\u{X}\right)$.

Let $^1 \mathcal{X}$ and $^1\mathcal{Y}$ be two Disk #1 material particles, that are initially located at $^1X$ and $^1Y$, with position vectors $^1 \u{X}$ and $^1\u{Y}$, respectively. Let $^1 \u{X}-\,^1 \u{Y}=\u{E}_1$. At time $\u{t}$ they are located at $o+\u{x}_{\u{t}}(^1 \u{X})$ and $o+\u{x}_{\u{t}}(^1 \u{Y})$. We call the vector \(^1\u{e}_1(\u{t}):=\u{x}_{\u{t}}(^1 \u{X})-\u{x}_{\u{t}}(^1 \u{Y})\) the co-rotational vector on Disk 1 corresponding to $\u{E}_1$. It can be shown that \(^1\u{e}_{j}(\u{t})=\lurd{1}{\u{R}}{\u{t}}\u{E}_i\) At $\u{t}=\u{0}$, we have that

\[\begin{align} ^1\u{e}_{j}(\u{0})&=\lurd{1}{\u{R}}{\u{0}}\u{E}_i,\\ &=\u{E}_i \end{align}\]

Say that $^1\u{e}_i(\u{t})$ be the vectors fixed to the Disk #1. That is they move with Disk 1. These are called the co-rotational basis vectors.

Also let $^1\mathcal{O}$ be a particle on Disk #1. Initially it is located at $o+\lu{1}{\u{O}}(\u{0})$. As the Disk 1 moves, it moves with it. At time $\u{t}$ it is located at $\lu{1}{o}(\u{t})$. Or more explicitly,

\(\begin{align} \lu{1}{o}(\u{t})&=o+\lu{1}{\u{O}}(\u{t})\\ \u{O}(\u{t})&=\u{x}_{\u{t}}\left(^1\u{O}(\u{0})\right)\\ \lu{1}{\u{O}}(\u{t})&:=^1\!\!\u{R}_{\u{t}}\, ^1\u{O}(\u{0})+\lu{1}{\u{c}}(\u{t}) \end{align}\) The vectors $(^1\u{e}_i(\u{t}))$ and the point $^1o(\u{t})$ taken together define a moving co-ordinate frame. We would need the reprsentation of the last equation in component form. So, introducing $\lu{1}{\u{c}}(\u{t})=\lurd{1}{c}{m}(\tau)\u{e}_m$ and $\lu{1}{\u{O}}(\u{0})=\lurd{1}{o}{n}\u{e}_n$, and $\lurd{1}{\u{R}}{\u{t}}=\lurd{1}{R}{mj}(\tau)\u{e}_m\otimes \u{e}_j$, we get that

\[\begin{align} \lu{1}{\u{O}}(\u{t})&=\lurd{1}{R}{mj}(\tau)\u{e}_m\otimes\u{e}_j \, \lurd{1}{o}{n}\u{e}_n+\lurd{1}{c}{m}(\tau)\u{e}_m\\ &=\pr{\lurd{1}{R}{mj}(\tau) \lurd{1}{o}{j}+\lurd{1}{c}{m}(\tau)}\u{e}_m \end{align}\]

Let the Disk 2’s materials particle particle $\lu{2}{\mathcal{X}}$ at times $\u{t}=\u{0}$ be located at $^1o(\u{0})+\u{x}$, i.e., at $o+\lu{1}{\u{O}}+\u{x}$. Say $\u{x}=x_i\,\lurd{1}{\u{e}}{i}(\u{0})$. At time $\u{t}=\u{0}$ the $\lurd{1}{\u{e}}{i}(\u{0})=\u{E}_i$, we have that $\u{x}=x_i \u{E}_i$. Let $\lu{1}{\u{O}}(\u{0})=\lurd{1}{o}{i}(\tau)\u{E}_i$. Thus the position vector of $\lu{2}\mathcal{X}$ at $\u{t}=\u{0}$ is $(\lurd{1}{o}{i}(0)+x_i)\u{E}_i$. Knowing the position vector of $\lu{2}{\mathcal{X}}$ at time $\u{t}=\u{0}$, the components $x_i$ can be computed easily.

The motion of the (purple) Disk #2 with respect to Disk #1 is given as \(\u{y}_{\u{t}}(\u{x})=\lurd{2}{\u{R}}{\u{t}} \u{x}+\lu{2}{\u{c}}(\u{t}).\)

The above statement means that the Disk 2’s particle $\lu{2}{\mathcal{X}}$ that was initially located at $^1o(\u{0})+\u{x}$ is located at the point $^1o(\u{t})+\u{y}_{\u{t}}(\u{x})$ at the time instance $\u{t}$. To be move explicit, at the time instance $\u{t}$ the material particle $\lu{2}{\mathcal{X}}$ is at the spatial point

\[\begin{align} \lu{2}{x}(\u{t})&=\lu{1}{o}(\u{t})+\lurd{2}{\u{R}}{\u{t}}\u{x}+\lu{2}{\u{c}}(\u{t})\\ &=o+ \lu{1}{\u{O}}(\u{t})+\lurd{2}{\u{R}}{\u{t}}\u{x}+\lu{2}{\u{c}}(\u{t}) \end{align}\]

Let

\[\begin{align} \lurd{2}{\u{R}}{\u{t}}&=\lurd{2}{R}{ij}(\tau)\lurd{1}{\u{e}}{i}(\u{t})\otimes \lurd{1}{\u{e}}{i}(\u{0})\\ &=\lurd{2}{R}{ij}(\tau)\lurd{1}{\u{e}}{i}(\u{t})\otimes \u{e}_j\\ &=\lurd{2}{R}{ij}(\tau)\pr{\lurd{1}{\u{R}}{\u{t}}\u{e}_i}\otimes \u{e}_j\\ &=\lurd{2}{R}{ij}(\tau)\pr{\lurd{1}{R}{mn}(\tau)\u{e}_m\otimes \u{e}_n\u{e}_i}\otimes \u{e}_j\\ &=\lurd{2}{R}{ij}(\tau)\pr{\lurd{1}{R}{mn}(\tau)\u{e}_m\delta_{ni}}\otimes \u{e}_j\\ &=\lurd{2}{R}{ij}(\tau)\pr{\lurd{1}{R}{mi}(\tau)\u{e}_m}\otimes \u{e}_j\\ &=\lurd{1}{R}{mi}(\tau)\lurd{2}{R}{ij}(\tau)\u{e}_m\otimes \u{e}_j\\ \end{align}\] \[\begin{align} \lurd{2}{\u{R}}{\u{t}}\u{x}&= \lurd{1}{R}{mi}(\tau)\lurd{2}{R}{ij}(\tau)\u{e}_m\otimes \u{e}_j x_k \u{e}_k\\ &=\lurd{1}{R}{mi}(\tau)\lurd{2}{R}{ij}(\tau)\u{e}_m \delta_{jk} x_k \\ &=\pr{\lurd{1}{R}{mi}(\tau)\lurd{2}{R}{ij}(\tau) x_j} \u{e}_m\\ \end{align}\]

Say $\lu{2}{\u{c}}(\u{t})=\lurd{2}{c}{i}(\tau)\lurd{1}{\u{e}}{i}(\u{t})$. Then we get that

\[\begin{align} \lu{2}{\u{c}}(\u{t})&=\lurd{2}{c}{i}(\tau)\lurd{1}{\u{R}}{\u{t}}\u{e}_i\\ &=\lurd{2}{c}{i}(\tau)\lurd{1}{R}{mn}(\tau)\u{e}_{m}\otimes \u{e}_n\u{e}_i\\ &=\lurd{1}{R}{mi}(\tau)\lurd{2}{c}{i}(\tau)\u{e}_{m}\\ \end{align}\]

Combining the last two results we get That \(\begin{align} \lurd{2}{\u{R}}{\u{t}}\u{x}+\lu{2}{\u{c}}(\u{t})&= \pr{\lurd{1}{R}{mi}(\tau)\lurd{2}{R}{ij}(\tau) x_j+\lurd{1}{R}{mi}(\tau)\lurd{2}{c}{i}(\tau)}\u{e}_{m}\\ &=\lurd{1}{R}{mi}(\tau)\pr{\lurd{2}{R}{ij}(\tau) x_j+\lurd{2}{c}{i}(\tau)}\u{e}_{m} \end{align}\)

\[\begin{align} \lu{1}{\u{O}}(\u{t})+\lurd{2}{\u{R}}{\u{t}}\u{x}+\lu{2}{\u{c}}(\u{t})&= \lurd{1}{R}{mi}(\tau)\pr{\lurd{2}{R}{ij}(\tau) x_j+\lurd{2}{c}{i}(\tau)}\u{e}_{m}+\pr{\lurd{1}{R}{mj}(\tau) \lurd{1}{o}{j}+\lurd{1}{c}{m}(\tau)}\u{e}_m\\ &=\lurd{1}{R}{mi}(\tau)\pr{\lurd{2}{R}{ij}(\tau) x_j+\lurd{2}{c}{i}(\tau)}\u{e}_{m}+\pr{\lurd{1}{R}{mi}(\tau) \lurd{1}{o}{i}+\lurd{1}{c}{m}(\tau)}\u{e}_m\\ \end{align}\]