\[\newcommand{\u}[1]{\boldsymbol{\mathsf{#1}}} \renewcommand{\b}[1]{\boldsymbol{#1}} \newcommand{\t}[1]{\textsf{#1}} \newcommand{\m}[1]{\mathbb{#1}} \def\RR{\bf R} \def\bold#1{\bf #1} \def\mbf#1{\mathbf #1} \def\uv#1{\hat{\usf {#1}}} \def\dl#1{\underline{\underline{#1}}} \newcommand{\usf}[1]{\boldsymbol{\mathsf{#1}}} \def\bs#1{\usf #1}\]

Cylindrical Co-ordinates

The cylindrical basis vectors consist of the vectors {$\boldsymbol{e}_r, \boldsymbol{e}_{\theta}, \boldsymbol{e}_z$}.

• The $\boldsymbol{e}_z$ points in a fixed direction in space. The plane orthogonal to the $\boldsymbol{e}_z$ vector points in the xy plane.
• The radial vector points from the origin to the particle’s projection in the xy plane.
• The vector $\boldsymbol{e}_\theta$ is perpendicular to both $\boldsymbol{e}_r$ and $\boldsymbol{e}_z$ such that {$\boldsymbol{e}_r, \boldsymbol{e}_{\theta}, \boldsymbol{e}_z$} form an orthogonal triad.

The position vector of particles can be written as \(\begin{align} \boldsymbol{r} = R\boldsymbol{e}_r + z\boldsymbol{e}_z \end{align}\)

The reason $\boldsymbol{e}_\theta$ doesn’t show up in the above relation is because we have the following relation between the Cylindrical and Cartesian co-ordinates, \(\begin{align} R &= (x_1^2 + x_2^2)^{1/2} \\ \boldsymbol{e}_r &= \cos[\theta]\boldsymbol{e}_1 + \sin[\theta]\boldsymbol{e}_2 \\ \boldsymbol{e}_\theta &= -\sin[\theta]\boldsymbol{e}_1 + \cos[\theta]\boldsymbol{e}_2 \end{align}\)

Derivatives of $\boldsymbol{e_r}$ and $\boldsymbol{e}_\theta$

Using the Cartesian representation, we have that \(\begin{align} \frac{d\boldsymbol{e}_r}{d\theta} &= -\sin[\theta]\boldsymbol{e}_1 + \cos[\theta]\boldsymbol{e}_2 \\ &= \boldsymbol{e}_\theta\\ \frac{d\boldsymbol{e}_\theta}{d\theta} &= -\cos[\theta]\boldsymbol{e}_1 - \sin[\theta]\boldsymbol{e}_2 \\ &= \boldsymbol{e}_r\\ \end{align}\) So we have \(\begin{align} \boldsymbol{v} = \dot{\boldsymbol{r}} &= \dot{R}\boldsymbol{e}_r + R\dot{\boldsymbol{e}_r} + \dot{z}\boldsymbol{e}_z ,\\ \boldsymbol{v} &= \dot{R}\boldsymbol{e}_r + R\dot{\theta}{\boldsymbol{e}_\theta} + \dot{z}\boldsymbol{e}_z. \end{align}\) For acceleration, \(\begin{align} \dot{v} &= \ddot{R}\boldsymbol{e}_r + \dot{R}\dot{\boldsymbol{e}_r} + \dot{R}\dot{\theta}\boldsymbol{e}_\theta + R\ddot{\theta}\boldsymbol{e}_\theta + R\dot{\theta}\dot{\boldsymbol{e}_\theta} + \ddot{z}\boldsymbol{e}_z \\ &= (\ddot{R} - R\dot{\theta}^2)\boldsymbol{e}_r + (2\dot{R}\dot{\theta} + R\ddot{\theta})\boldsymbol{e}_\theta + \ddot{z}\boldsymbol{e}_z \end{align}\)

Car travelling to top of mountain example

Question: A car travels with constant speed v on a spiraling path along a mountain. The shape of the mountain is approximated as a paraboloid with base radius a and height h. It takes the car exactly six full turns around the mountain to reach the top. Find the velocity of the car as a function of its radial distance R from the center of the mountain.

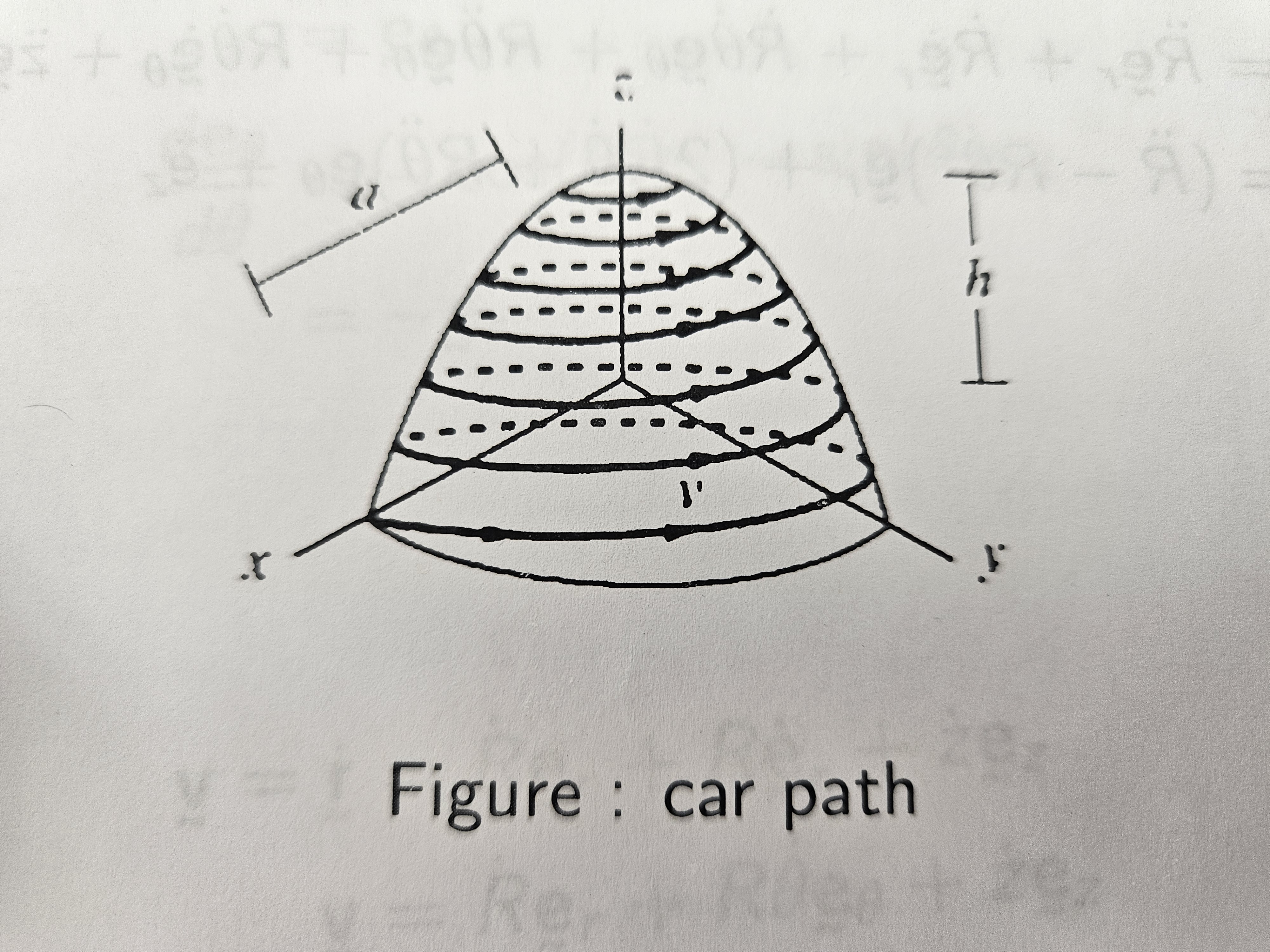
Assume that the car climbs such that z $\propto \theta$. Find v = f($\dot{R}$)

Solution:

From the given conditions, we get two equations for z \(\begin{align} z &= \frac{h}{12\pi}\theta \\ z &= h \left(1-\frac{R^2}{a^2}\right) \end{align}\)

U\sing the equation of velocity (10) and the two equations (13) and (14), we get \(\begin{align} v &= \dot{R}\left(1 + 576\pi^2\frac{R^4}{a^4} + 4h^2\frac{R^2}{a^4}\right)^{1/2} \end{align}\)