[edit]

Beginner’s Guide to Mathematica

Mathematica is a software application that goes beyond numeric and symbolic calculations. It is a modern technical computing system based on a high-level general-purpose programming language, the Wolfram Language. The Wolfram Language kernel is a text-based interface that allows you to evaluate Wolfram Language commands.

Useful resources:

• Wolfram Language & System Documentation Center
• Symbolic Notational Forms on how to input subscripts, superscrits, underbar, overbar and so on.
• Special Characters on how to input special characters.
• Hands-on Start to Mathematica
• The Wolfram Language: FAST INTRODUCTION FOR PROGRAMMERS
• An Elementary Introduction to the Wolfram Language
• A collection of Mathematica learning resources at Stack Overflow

Mathematica files:

• Example (used in this tutorial)
• HW #1 Solution (learn how to define symbolic notations and perfrom operations on vectors and tensors)

Input and output cells

• After launching Mathematica, you will see the input screen, called a Notebook. Mathematica Notebooks are comprised of cells. When you begin typing commands, you’ll notice that brackets appear on the right side of the notebook. These are called cell brackets. These cells are labeled In[1], Out[1], In[2], and so on.

• To evaluate the expression, press Shift+Enter in the input cell. Press Enter, instead, to create a new line in the input cell.

• Use a semicolon after the expression to suppress the output.

• To abort the evaluation, choose Abort Evaluation from the Evaluation menu, or press Alt+. (Win OS) or Command+. (Mac OS).

• Group cells that groups the input and output cells together.

• Double click on the bracket of the group to hide and redisplay the group cells.

Comments

• Comments are delimited by (* *).

Variable names

• Variable names cannot begin with numbers, e.g., 5name is not allowed; But otherwise numbers can occur and there is no restriction on the length of a name, e.g., alpha123, beta, lambda, etc.

• Mathematica is case sensitive, e.g., the variable abc is not the same as Abc.

• No need to say, the user-defined variable names should not be the Mathematica built-in names.

Clear variables

• Use the Clear command or =. to remove any variable definitions, e.g., Clear[x, y] clears the values stored by variables x and y, and a=. removes the definition of a.

• Use the command Clear[“Global`*”] to clear all variables.

• Choose Quit Kernel from the Evaluation menu to quit the kernel, which clears all the defined variables.

Important conventions

• All Mathematica commands begin with a capital letter, such as Sin, Cos, Table, Integrate, Plot, etc.

• The standard arithmetic operations are +, -, *, /, and ^.

• Function arguments are always enclosed by square brackets, [ ], e.g., Sin[x], Sqrt[x], Log[x], Max[x], etc.

• Parentheses, ( ), are used to group objects together, thus establishing priority of operations, e.g., (3+4)/2, which is different from 3+4/2.

• Lists are enclosed by braces, { }, e.g., x = {1,2,5,7}. List elements are accessed via double square [[ ]], e.g., x[[3]], which refers to the third element of list x.

• A space is interpreted as multiplication. Sometimes even a space is unnecessary, e.g., 2a and 2Sin[x] work as expected, but xy is not the same as x*y.

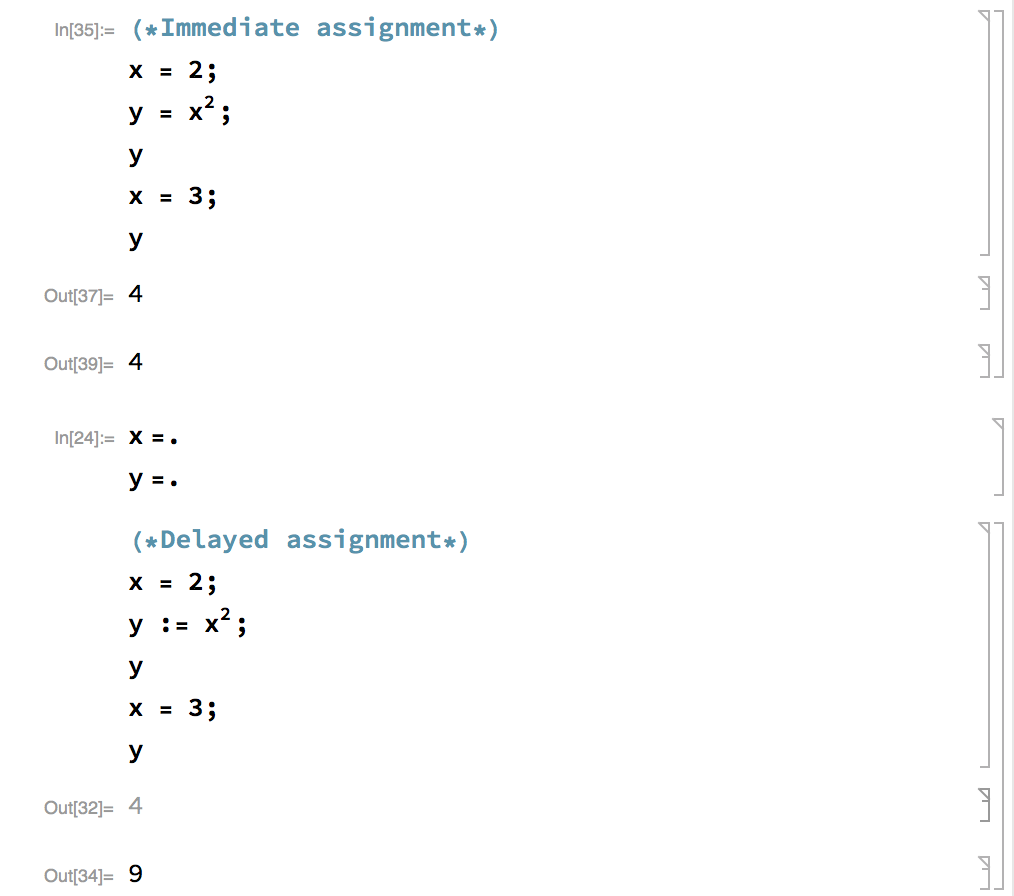
• There are three usages of the equal sign.

  • Immediate assignment =. The ordinary assignment of one value to a variable, e.g., a = 5.

  • Delayed assignment, which is identified by :=, e.g., y := x. The difference between immediate and delayed assignments is:

  • Operators used to represent two expressions are equal to each other (==), e.g., expr1 == expr2.

Frequently used built-in functions

Mathematica has over 5000 built-in functions. Here is an alphabetical listing of these functions.

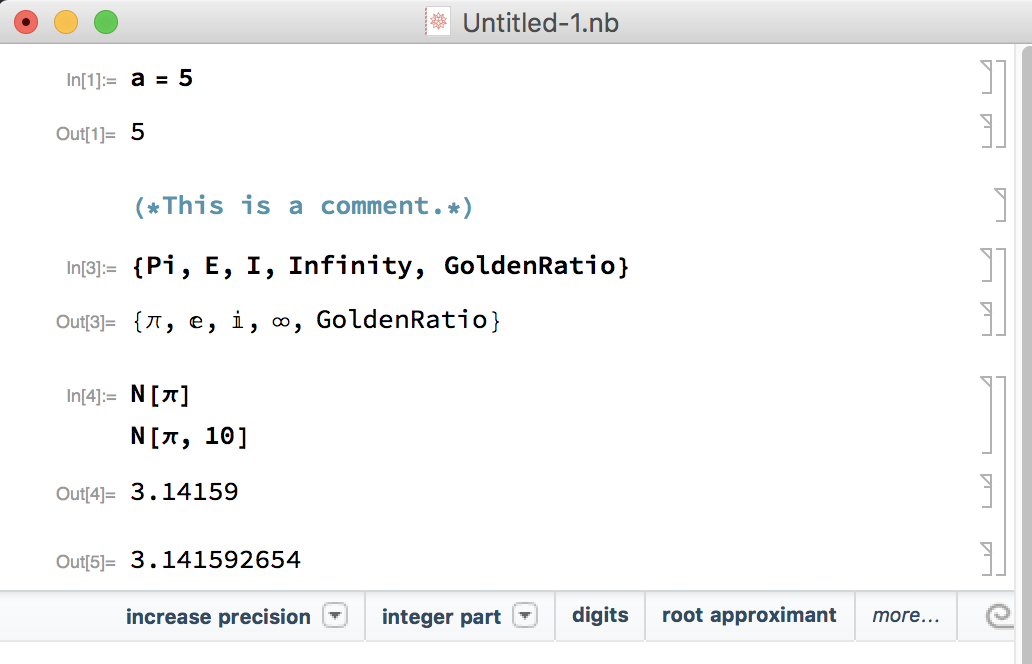
• The basic constants are PI, E, I, Infinity and GoldenRatio. To turn a symbolic value into a numeric one, use N[ ]. N[x, d] returns d significant digits.

• The basic functions include Log, Exp, Sin, Cos, Tan, Cot, Sec, Csc, ArcSin, ArcCos, ArcTan, and so on.

• To graph the functions, we could use the Plot function. 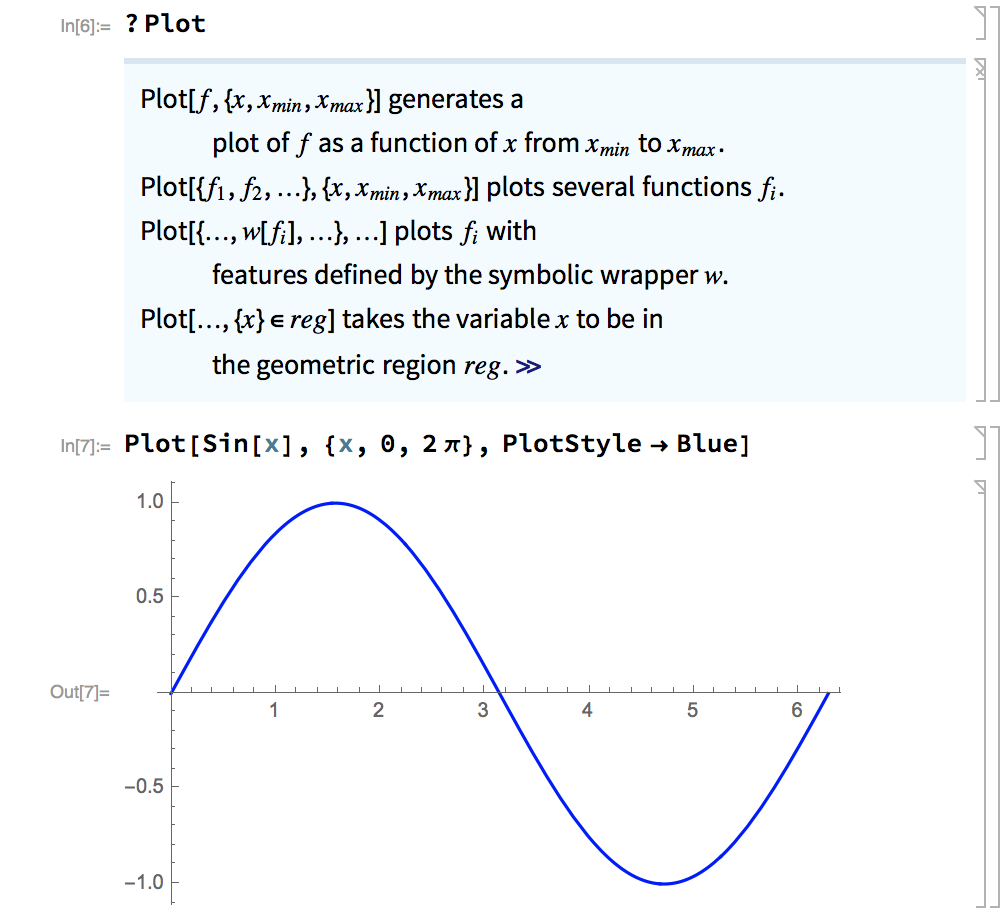We can use ? followed by a command to quickly look up the usage of this command.

• Simplify[] tries to convert the expression into a simpler form, limited to pain algebraic manipulation.

• FullSimplify also tries procedures using various functions.

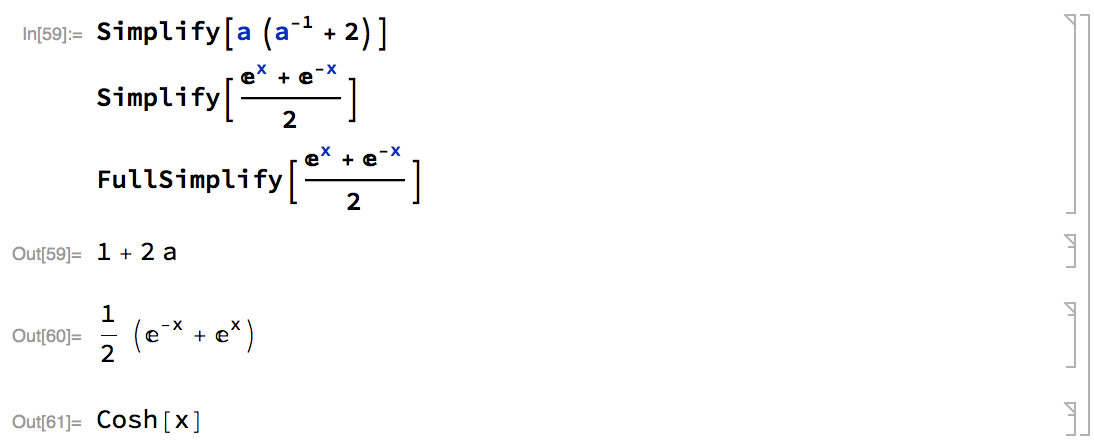
• Solve[expr,vars] find the solution of the system of equations.

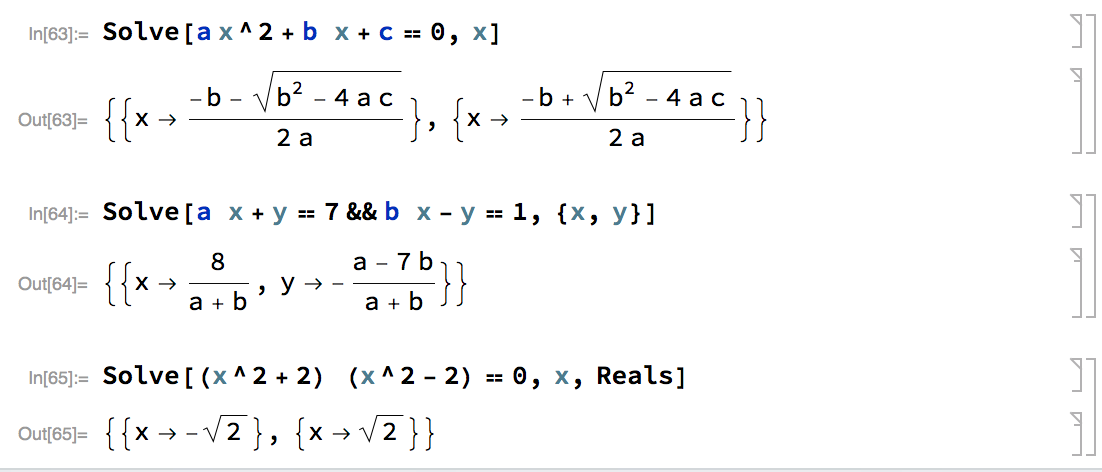
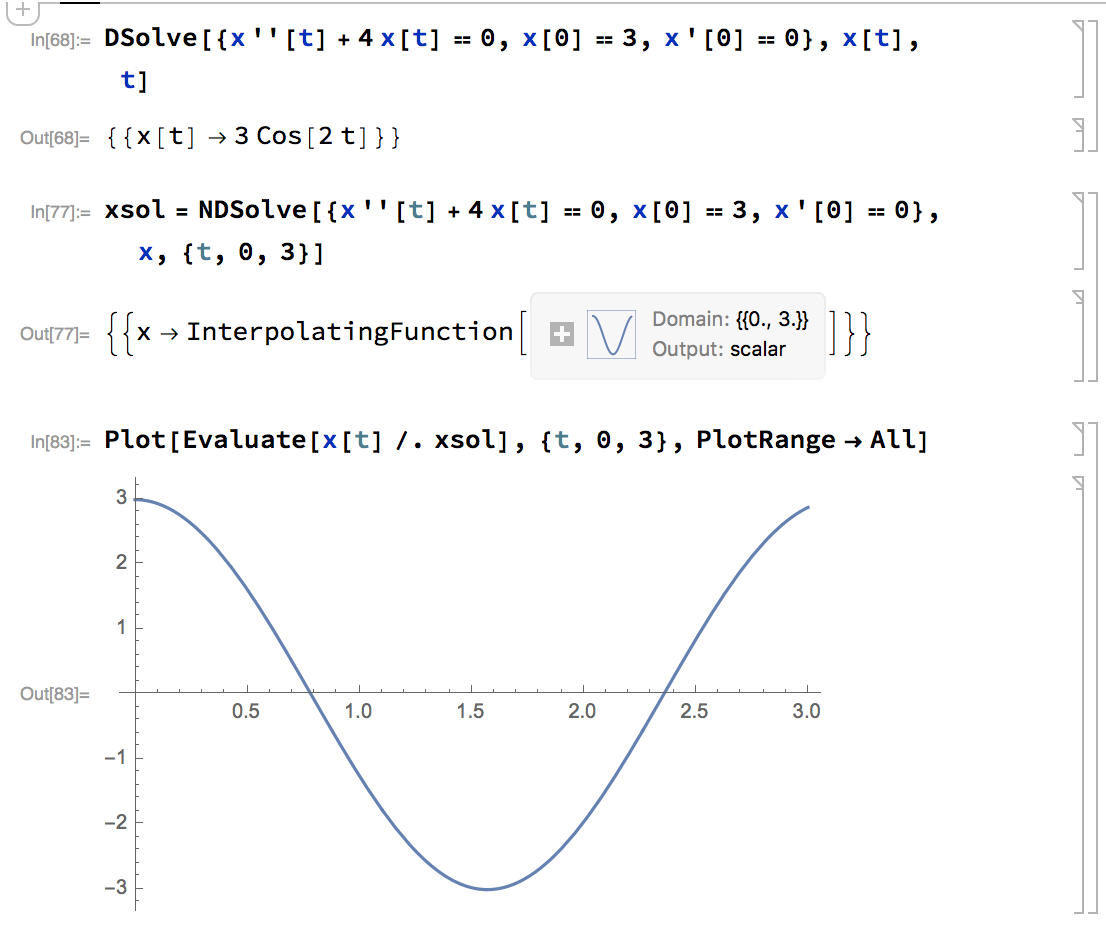
• DSolve[eqns,\(u\),\(x\)] solves a differential equation for the function \(u\), with independent variable \(x\).

• NDSolve[eqns,\(u\),{\(x, x_{min}, x_{max}\)}] finds a numerical solution to the ordinary differential equations eqns for the function \(u\) with the independent variable \(x\) in the range \(x_{min}\) to \(x_{max}\).

• D[\(f,x\)] gives the partial derivative.

• Integrate[\(f,x\)] gives the indefinite integral.

• Sum[\(f\),{\(i, i_{min}, i_{max}\)}] evaluate the sum.

Replacement operator

• The replacement operator (/.) is used to replace a variable with other variables or expressions. To get the right arrow, use a minus sign, then greater than (->).

Postfix Functions

• The standard function call is function name[expression/arguments], e.g., N[x], Simply[a(1/a+2)], Expand[(x+1)^2], etc.
• Use postfix calls (//) to call a function: expression // function name, e.g., x // N, a(1/a+2)//Simply, (x+1)^2//Expand, etc.

Defining your own functions

It is fairly straight forward to define your own functions in Mathematica. For example, we define the function \(f(x)\) as In this example,

• The function name is \(f\). It is recommended that you use function names that start with a lower case letter, so that they don’t get confused with names of built-in functions.

• The \(x\)_ is a pattern. The underscore ( _, called blank in Mathematica) means that \(x\)_ is a pattern object that can stand for any Wolfram Language expression, i.e., replace \(x\) with anything inside the square bracket [] when calling the function \(f\).

• := set delay assignment. The set delay assignment is essential for a function.

• Now we can call the function \(f\).

Flow control

• If[condition,t,f] gives t if condition evaluates to True, and f if it evaluates to False.

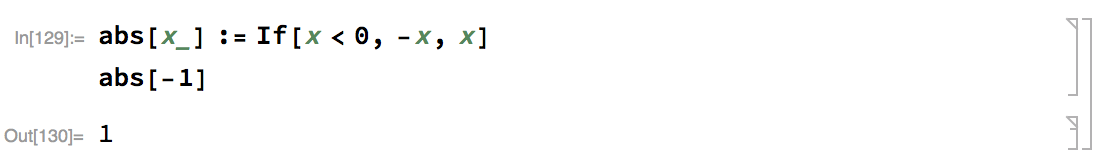
• For[start,test,incr,body] executes start, then repeatedly evaluates body and incr until test fails to give True. 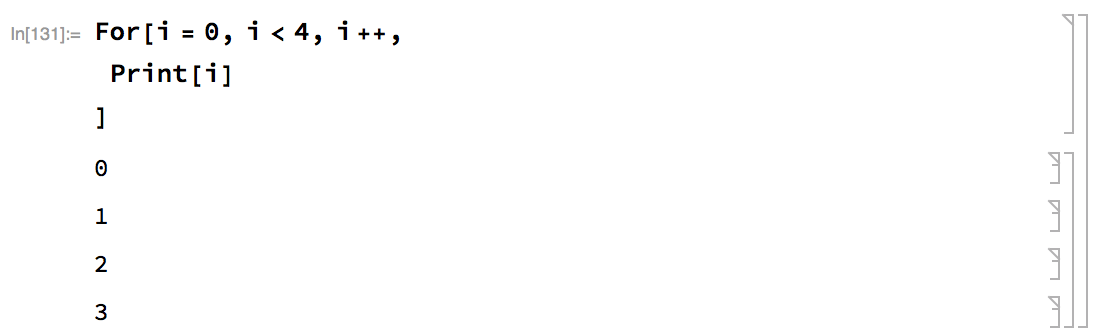Here \(i++\) is equivalent to \(i = i + 1\).

• While[test,body] evaluates test, then body, repetitively, until test first fails to give True.

Lists

Lists are used as the basic method of collecting numbers, symbols, and other objects. In addition, vectors and matrices are, in fact, lists.

Lists in Mathematica are surrounded by braces { }, and matrices are just lists of lists, all having the same length. Note that a list here is a computer list, so that {a, b} is the ordered pair (a, b), unlike classic mathematical usage where {a, b} denotes the set consisting of a and b; thus in Mathematica, {a, b} is not identical to {b, a}.

Create lists

The most common way to generate a list is by using the command Table and Range.

• Table[expr, \(i, i_{min}, i_{max}, di\)] generates a list by evaluating the expr a number of times determined by the iterator list.

• Range[\(i_{min}, i_{max}, di\)] generates a list of ordered numbers starting from \(i_{min}\) and going up to, but not exceeding, \(i_{max}\) in incremental of \(di\).

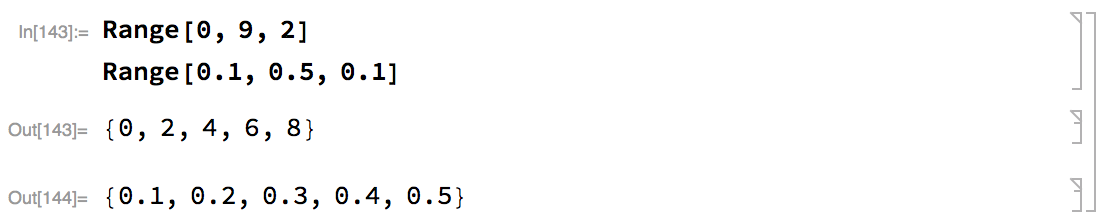
• We can also create a list by entering the list elements manually. For example, we define the vector and tensor as:

Display lists

• MatrixForm and TraditionalForm

• ListPlot

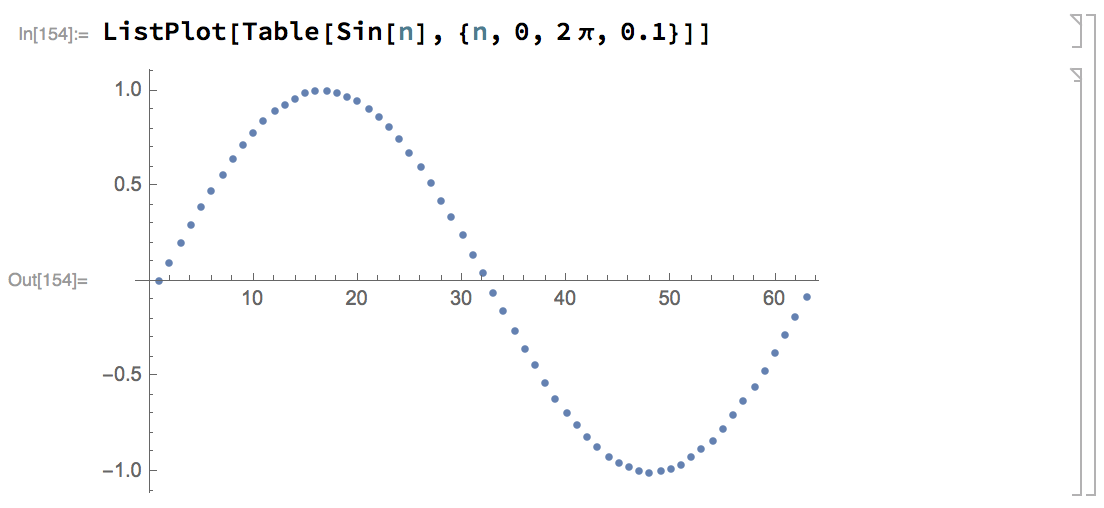
• MatrixPlot

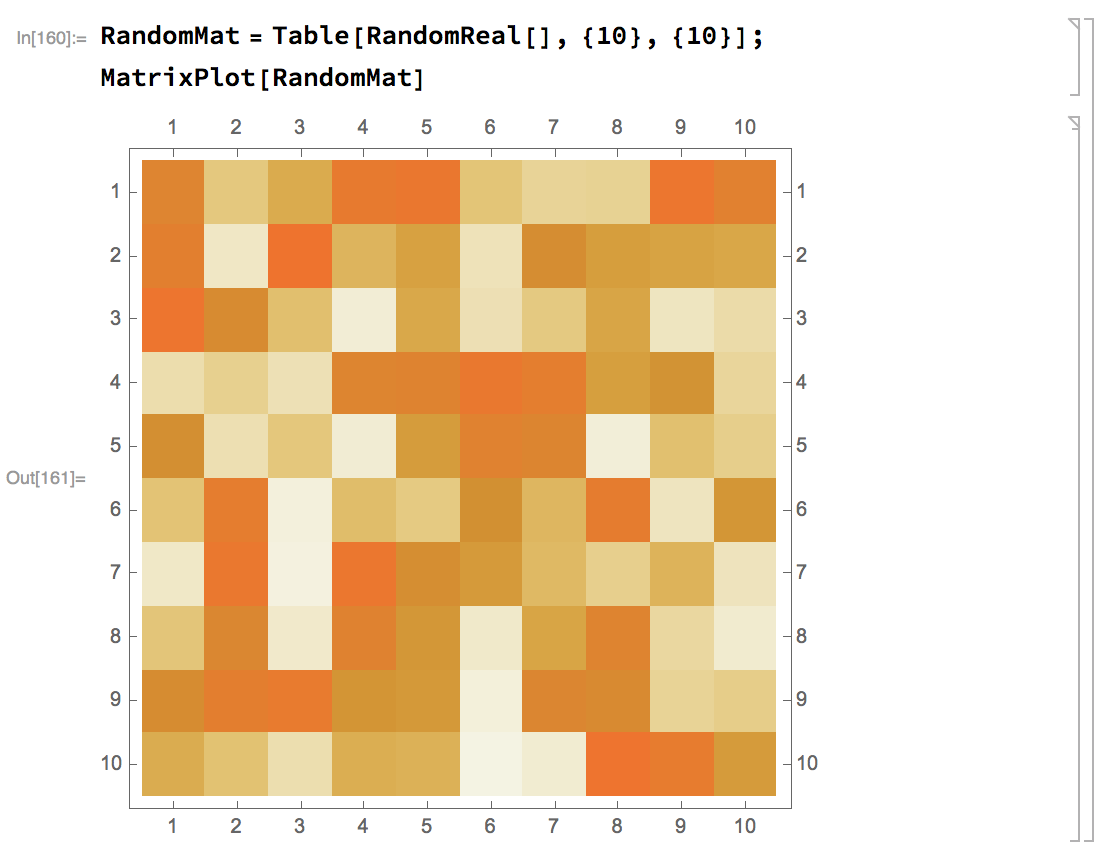
• SymmetricMatrixQ[m] gives True if m is explicitly symmetric, and False otherwise.

Operating on lists

• Length gives the length of the list.
• Normal operators (+ - * / ^) operate on each element by corresponding element.

• Dot (.) and cross product (x) of vectors.

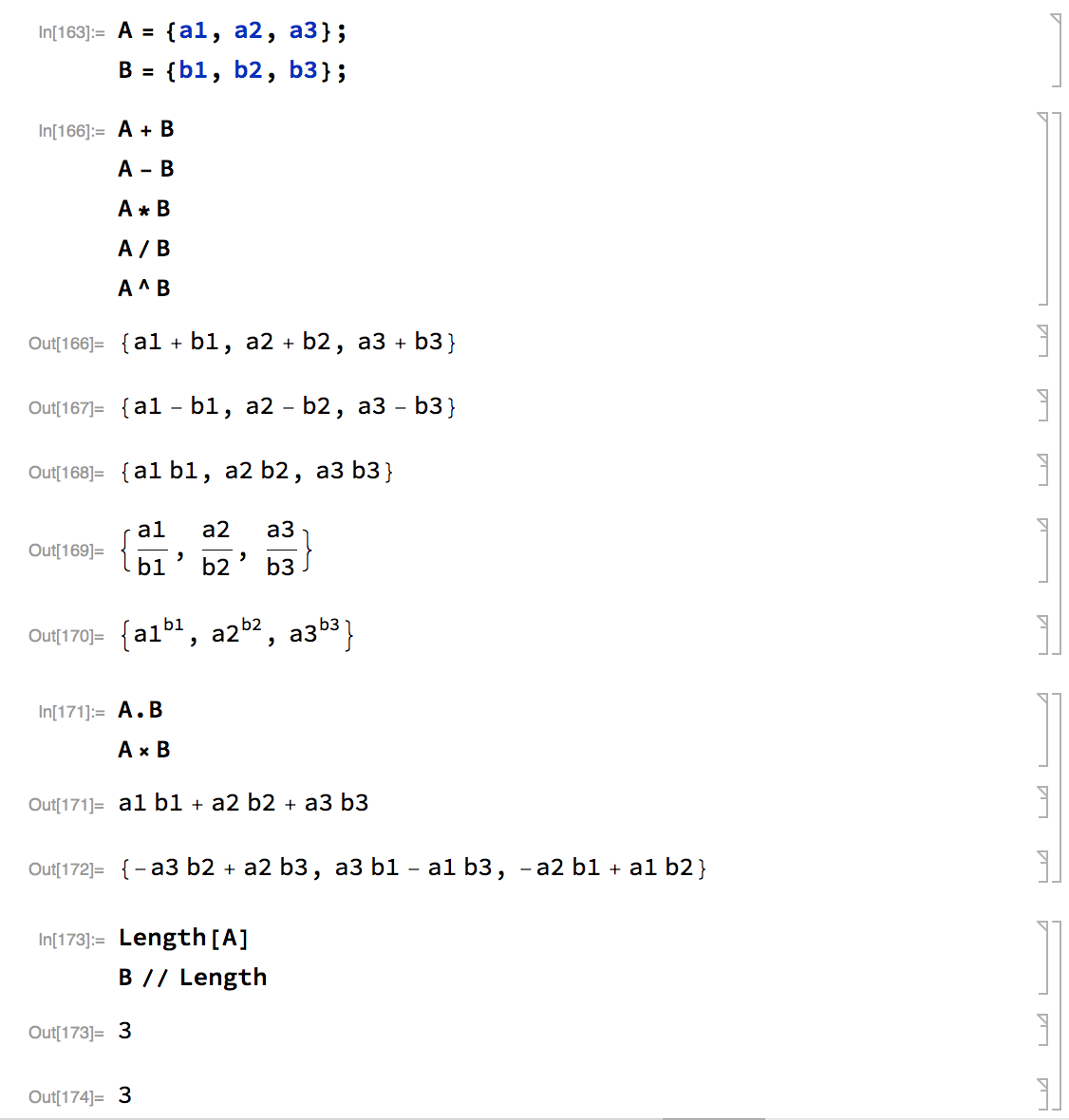
• Tensor multiplication (.).

• Indexing vectors and matrices ([[ ]]).

• Transpose of a matrix (Transpose[m]).

• Trace of a tensor (Tr[m]).

• Identity matrix (IdentityMatrix[n])

• Rotation matrix (RotationMatrix[θ]) gives the 2D rotation matrix that rotates 2D vectors counterclockwise by θ radians.