Advanced Mathematica

Important packages

This is some new information

Pop-out window showing variables in the workspace

Begin["frame`"];
CreateWindow@PaletteNotebook[{Button["Refresh", vars = Framed[
       Grid[
        Select[With[{expr = ToExpression@#}, {Which[ListQ[expr], #, 
              NumericQ[expr], #, True, expr], Head[expr],
             Which[
              ListQ[expr], Dimensions[expr],
              NumericQ[expr], expr,
              StringQ[expr], StringLength[expr],
              True, "-"]}] & /@ 
          Names["Global`*"], (#[[2]] =!= Framed ) &], 
        Alignment -> Left], FrameStyle -> None, FrameMargins -> 5]], 
    Dynamic[vars]}, WindowElements -> {"VerticalScrollBar"}, 
   WindowTitle -> "Global`*"];
End[];

Hide/Show Input/Output/Text/Initialization and Delete Output

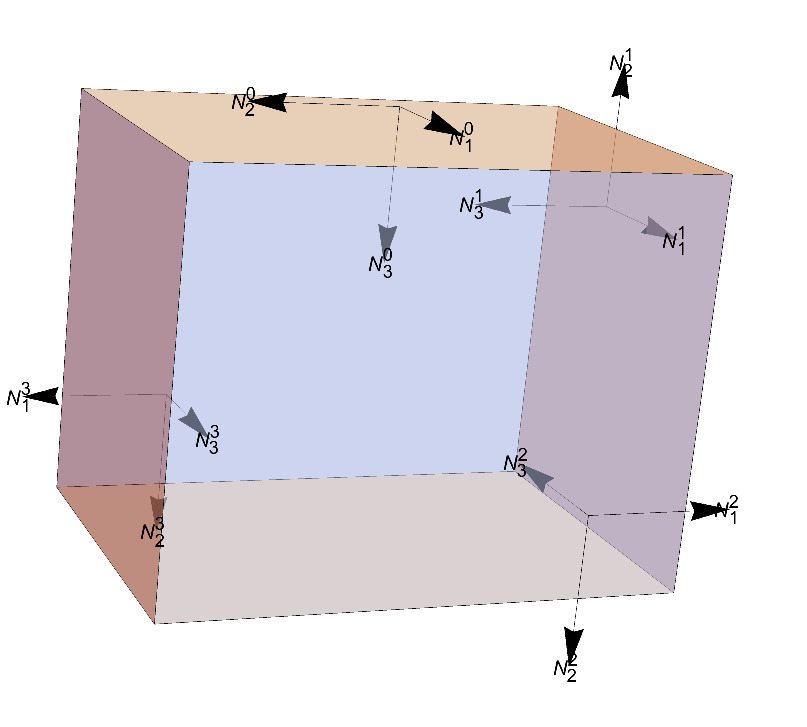
Create a Box and arrows

Block[{\[Epsilon] = 0.1, \[Tau] = 0.9, 
  pmin = \[Tau] {-(l1/2), -(b1/2), -(h1/2)}, 
  pmax = \[Tau] {l1/2, b1/2, h1/2}},
 Graphics3D[{
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)N\), \(_\
\)]\) [[1]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(1\), \(0\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)N\), \(_\
\)]\) [[1]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)N\), \(_\
\)]\) [[2]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(2\), \(0\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)N\), \(_\
\)]\) [[2]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)N\), \(_\
\)]\) [[3]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(3\), \(0\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(0\)]\)N\), \(_\
\)]\) [[3]]],
   \[Continuation]
   \[Continuation]
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)N\), \(_\
\)]\) [[1]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(1\), \(1\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)N\), \(_\
\)]\) [[1]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)N\), \(_\
\)]\) [[2]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(2\), \(1\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)N\), \(_\
\)]\) [[2]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)N\), \(_\
\)]\) [[3]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(3\), \(1\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(1\)]\)N\), \(_\
\)]\) [[3]]],
   \[Continuation]
   \[Continuation]
   \[Continuation]
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)N\), \(_\
\)]\) [[1]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(1\), \(2\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)N\), \(_\
\)]\) [[1]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)N\), \(_\
\)]\) [[2]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(2\), \(2\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)N\), \(_\
\)]\) [[2]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)N\), \(_\
\)]\) [[3]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(3\), \(2\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(2\)]\)N\), \(_\
\)]\) [[3]]],
   \[Continuation]
   \[Continuation]
   \[Continuation]
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)N\), \(_\
\)]\) [[1]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(1\), \(3\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)N\), \(_\
\)]\) [[1]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)N\), \(_\
\)]\) [[2]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(2\), \(3\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)N\), \(_\
\)]\) [[2]]],
   Arrow[{
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) , 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)N\), \(_\
\)]\) [[3]]}],
   Text["\!\(\*SubsuperscriptBox[\(N\), \(3\), \(3\)]\) ", 
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)X\), \(_\
\)]\) + \[Epsilon]  
\!\(\*UnderscriptBox[\(
\(\*SuperscriptBox[\(\[InvisiblePrefixScriptBase]\), \(3\)]\)N\), \(_\
\)]\) [[3]]],
   {Opacity[0.5], Cuboid[pmin, pmax]}
   }, Boxed -> False
  ]
 ]

Mathematica Gist

Create a duplicate of a notebook

CreatePalette[
  Button["Duplicate Active Notebook", 
   NotebookPut[
    NotebookGet[
      InputNotebook[]] /. {Rule[DockedCells, _] :> Sequence[], 
      Rule[WindowMargins, _] :> 
       Rule[WindowMargins, { 0, 0 }], 
      Cell[x___] :> Cell[x, Evaluatable -> False]}, 
    Background -> GrayLevel[0.95], Editable -> False, 
    "ClosingSaveDialog" -> False, 
    DockedCells -> 
     With[{sourcenb = InputNotebook[]}, 
      Cell[BoxData[
        ToBoxes[Button["Update", 
          SelectionMove[InputNotebook[], All, Notebook];
          
          NotebookWrite[InputNotebook[], 
           NotebookGet[sourcenb] /. 
            Cell[x___] :> Cell[x, Evaluatable -> False]]]]], 
       "DockedCell", CellContext -> Cell]], 
    WindowTitle -> 
     "Duplicate of " <> 
      AbsoluteOptions[InputNotebook[], WindowTitle][[1, 2]]];
   SetSelectedNotebook[InputNotebook[]]], WindowTitle -> "Duplicate"];

Basic Notation for Mechanics Calculations

Get["Notation`"]; 
Symbolize[ParsedBoxWrapper[SubscriptBox["a_", "i_"]]]; 
Symbolize[ParsedBoxWrapper[OverscriptBox["a_", "."]]]; 
Symbolize[ParsedBoxWrapper[SuperscriptBox["e", "a_"]]]; 
Symbolize[ParsedBoxWrapper[UnderscriptBox["a_", "_"]]]; 
Symbolize[ParsedBoxWrapper[UnderscriptBox["a_", "_"]]]; 
Symbolize[ParsedBoxWrapper[SubscriptBox[
     RowBox[{"(", RowBox[{"a_", RowBox[{"(", "points", ")"}]}], ")"}], 
     RowBox[{RowBox[{"vertces", "=", "1"}], ",", "2", ",", "\[Ellipsis]"}]]]]; 
Symbolize[ParsedBoxWrapper[SubscriptBox[
     RowBox[{"(", RowBox[{"a_", RowBox[{"(", "t", ")"}]}], ")"}], 
     RowBox[{RowBox[{"t", "=", "0"}], ",", "\[CapitalDelta]t", ",", "\[Ellipsis]"}]]]]; 
Symbolize[ParsedBoxWrapper[SubscriptBox[RowBox[{"(", "a_", ")"}], 
     RowBox[{RowBox[{"t", "=", "0"}], ",", "\[CapitalDelta]t", ",", "\[Ellipsis]"}]]]]; 
Symbolize[ParsedBoxWrapper[SubscriptBox[
     RowBox[{"(", RowBox[{"a_", RowBox[{"(", "t", ")"}]}], ")"}], 
     RowBox[{"t", "=", "0"}]]]]; 
Notation[ParsedBoxWrapper[RowBox[{"\[LeftDoubleBracketingBar]", "a_", "\[RightDoubleBracketingBar]"}]] \[DoubleLongLeftRightArrow] 
    ParsedBoxWrapper[RowBox[{"Norm", "[", "a_", "]"}]]]; 

Delete all output cells

nb = EvaluationNotebook[]
NotebookDelete@Cells[nb, CellStyle -> "Output" || "Print" || "Echo"]

Repeated rule application for simplifying expressions

CustomRuleSimplify[expr_, rule_, n_: 1] := 
 If[n > 1, 
  NormSimplify[((expr /. rule) // Simplify), rule, 
   n - 1], (expr /. rule) // Simplify]

Clean Slate

<< Utilities`CleanSlate`
CleanSlate[]

Set notebook options, cell options, delete certain cells

SetHKNotebookOptions[nb_] := Module[{},
   SetOptions[nb, DockedCells -> {}, WindowFloating -> False];
   (*NotebookDelete@Cells[nb,CellStyle\[Rule]"Output" || "Print" || 
   "Echo"];*)
   
   SetOptions[NotebookFind[nb, #, All, CellStyle], 
      CellChangeTimes -> {}, ShowCellLabel -> True, 
      ShowCellTags -> False, ShowGroupOpener -> False] & /@ {"Input", 
     "Subsubsection"};
   
   NotebookDelete@Cells[nb, CellStyle -> "Output" || "Print" || "Echo"]
   ];

Usage: Set the options of two different notebooks to be the same before using NotebookDiff

nb1 = NotebookOpen[
   "/Users/hkesari/Downloads/Nov20_8noded_quads_parallel_energy_\
EnergyBugFixed_KVPosted.nb"];
nb2 = NotebookOpen[
   "/Users/hkesari/WebsitesHK/Curvilinear/OldFiles/Nov20_8noded_quads_\
parallel_energy_EnergyBugFixed_copy.nb"];
SetHKNotebookOptions[nb1]
SetHKNotebookOptions[nb2]

Analyzing differences between two notebooks

The below Mathematica code snippet open the tools to do NotebookDiff.

<<AuthorTools`
OpenAuthorTool[]

Closing output cells(maybe?)

nb=NotebookOpen@CloudObject["Calander18.nb"]
NotebookEvaluate[nb,InsertResults->True]
NotebookFind[nb,"Output",All,CellStyle]
FrontEndExecute[FrontEndToken[nb,"SelectionCloseUnselectedCells"]]
NotebookSave[nb] (*save notebook,identified by the notebook object "nb"*)
NotebookClose[nb] (*close notebook,identified by the notebook object "nb"*)

Plot[Sin[x],{x,-1,1}]
NotebookEvaluate[nb, InsertResults -> True]
NotebookFind[nb, "Output" , All, CellStyle]
FrontEndExecute[FrontEndToken[nb, "SelectionCloseUnselectedCells"]]

Creating new style sheets.

Mathematica Documentation Reference

Steps

Create Style Sheet

Open a new mathematica notebook. Let us call it template nb.
Modify Style Elements
- Open Format>Edit Style Sheet.
- The style sheet, ss, will have a title Private style settings for template nb
- In ss create all elements whose style you want to modify.
- Click on each of those elements and open Format>Option Inspection.
  - Inside option inspection you will be able to modify all the the different styles.
If any objects belonging to any of the elements whose style you have modifed in ss appear in template nb those objects will now show up with the updated style.
Save the note template nb somewhere
Now open ss again. And choose install style sheet. Leave the source slot unmodified. That is don’t choose either from clipboard or from file.
Give a appropriate name for the style sheet, say ss name.
Close ss
The style sheet ss name is saved in the system directories, such as,

/Users/Haneesh/Library/Mathematica/SystemFiles/FrontEnd/StyleSheets

StyleSheets>ls -l
total 1176
-rw-r--r--@ 1 Haneesh  staff   1.4K Dec 27 23:08 BlueSection.nb
-rwxr-xr-x@ 1 Haneesh  staff   4.1K Nov 26 20:09 MaTeXmaticaPlus.nb*
-rw-r--r--  1 Haneesh  staff   8.9K Dec 27 21:07 Slender.nb
-rw-r--r--@ 1 Haneesh  staff   1.1K Dec 27 23:00 StyleGreen.nb
-rw-r--r--@ 1 Haneesh  staff   1.2K Dec 27 21:15 StyleSlender.nb
-rw-r--r--  1 Haneesh  staff   553K Feb  2  2017 Tensorial.nb
StyleSheets>

You can now delete template nb if you like.
Testing
- Open a new notebook that you want to apply the style sheet ss to. Lets call it actual nb
- Once actual nb is open go to Format>Choose >Style Sheeet> ss name.
- That is it you are done.

Advanced Mathematica

Important packages

Pop-out window showing variables in the workspace

Hide/Show Input/Output/Text/Initialization and Delete Output

Create a Box and arrows

Create a duplicate of a notebook

Basic Notation for Mechanics Calculations

Delete all output cells

Repeated rule application for simplifying expressions

Clean Slate

Set notebook options, cell options, delete certain cells

Analyzing differences between two notebooks

Closing output cells(maybe?)

Creating new style sheets.

Steps

Create Style Sheet

Testing