This tutorial will take you all the steps required to

Set up and run a basic Abaqus simulation using Abaqus/CAE
Visualize the results and collect data

Here is how you simulate the ellipsoid deformation problem.

Open Abaqus/CAE. From the ‘Start Session’ menu select ‘With Standard/Explicit Model’ under ‘Create Model Database’.
To set up and run a simulation in CAE, you can either work through the various ‘Modules’ in the dropdown menu at the top of the screen, or you can click on the menus in the workflow tree on the left hand side of the screen. We will do the former in this tutorial.
The ‘Part’ module is used to define the geometry of the various interacting solids in the simulation. Here, we will create a sphere. Due to the symmetric property of the sphere in all three directions, we only create 1/8 of the geometry by revolution.
1. Select Part>Create from the top menu bar, then use the menu that comes up to name the part ‘Sphere’; Select ‘3D’ and ‘Deformable’ for the Modeling Space and ‘Revolution’ for the Type, and enter an Approximate size of 0.01.
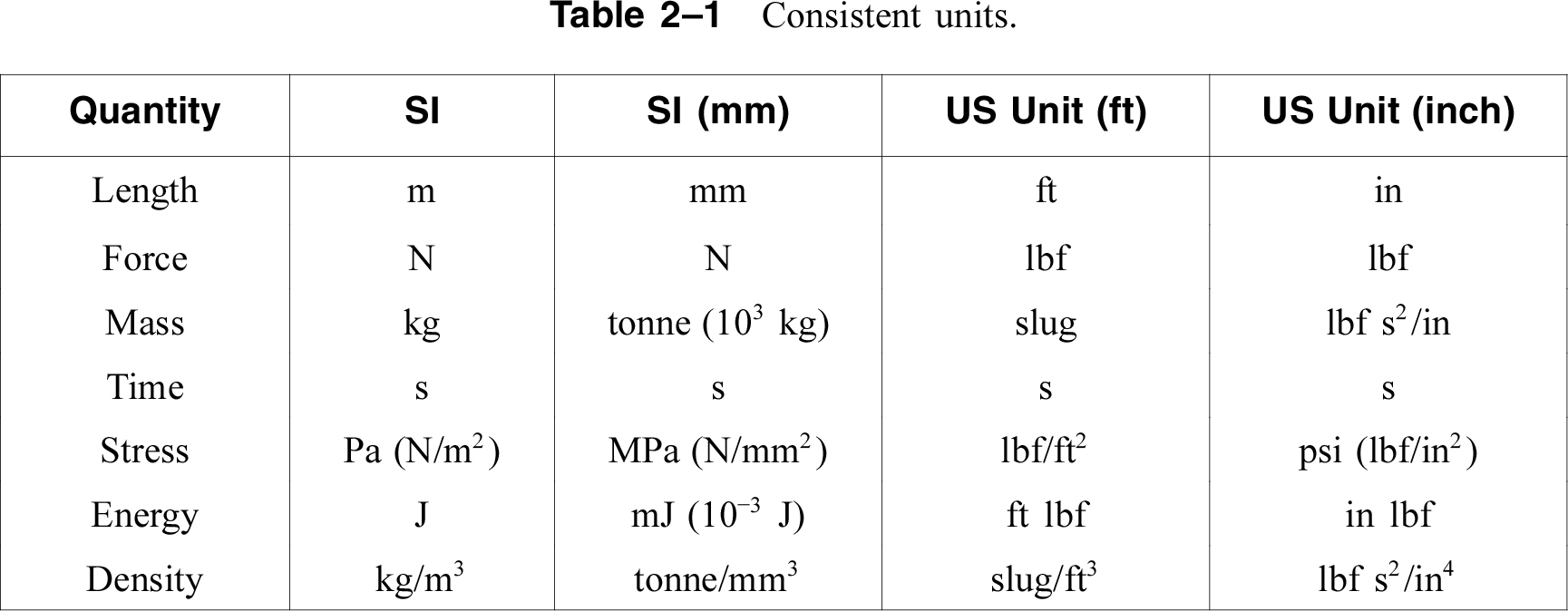
2. Use the sketch tools from the left to draw an 1/4 arc centered at (0,0), with a radius of 0.01837 (there is no explicit unit in Abaqus. You can use any self-consistent unit system. Here we use mm for length to avoid very small number. See the table below for consistent units). Use ‘Create Lines’ to close the 1/4 circular plate.
3. Exit the sketch menu by clicking ‘Done’ from the menu below.
4. In the popup ‘Edit Feature’ window, use the default parameters (Angle:90) and click ‘Apply’. You will see the 1/8 solid sphere.
Next, we will define material properties, and assign them to the parts.
1. Switch the ‘Module’ to ‘Property’.
2. To create a hyperelastic material, select ‘Create Material’. Change the name of the material to ‘Hyperelastic’. Select the Mechanical>Elasticity>Hyperelastic. In the menu that comes up select ‘Neo Hooke’ for the ‘Strain energy potential’, click the ‘Coefficients’ radio button, and enter a value of 2.75e-5 for C10 (the unit for stress is MPa) and 54545.5 for D1. This is for material with equivalent elastic constants 110 Pa for Young’s modulus and 0.0 for Poisson’s ratio. For the conversion, please look at the document.
3. Next, you have to create a ‘section’. This makes more sense for parts like beams or truss elements, where you need to define the geometry of the cross section, but you have to do it even for a 3D part. Select ‘Create Section’, then select Homogeneous Solid section from the menu, set the Material in the Edit Section menu as shown, then press OK.
4. Now you need to assign the created section to the geometry. Select ‘Assign Section’. Click on the sphere to select it (its edges should turn red), then select ‘Done’ from the bottom of the window. Click OK after you make sure that the name of the Section is what you just created. This has now assigned the hyperelastic material model to the part representing the sphere (shown green color). If you want to make a part heterogeneous, you can partition it, and assign different properties to the different partitions.
Now we create an assembly of the parts.
1. Switch the ‘Module’ to ‘Assembly’.
2. Select ‘Create Instance’.
3. On the menu select the Sphere; Check the ‘Independent’ radio button.
Set up a working directory abd save the model database to a file named ‘SphereToEllipsoid.cae’.
Next, we define the ‘Step’, which specifies the time interval of the simulation, as well as various options defining the finite element algorithms. The ‘Step’ module is also used to define variables that will be saved to the output database during analysis.
1. Select the Step module. Select ‘Create Step’ from the panel.
2. In the menu that appears select ‘Static,General’.
3. On the next menu, check on the NLGEOM box (this will ensure ABAQUS runs as finite strain computation). You can leave the other options at their default values, but take a look at the tabs to see what the Step menu allows you to control.
4. The Step module also allows you to select variables to write to the database. In this example, we will set up Abaqus to save the Shear traction vector (TRSHR) and Normal component of the traction vector (TRNOR). Click on the top menu Output>Field Output Request> Create. Then, in the Edit Field Output Request menu, find TRSHR and TRNOR in the fold of ‘Forces/Reactions’. Finally, press OK.
Next, we specify boundary conditions for the analysis. Switch to the ‘Load’ module.
1. To enforce the symmetry boundary conditions in three directions, select BC>Create; then in the Create Boundary Condition menu, name the boundary condition xsym; select the initial step; the Mechanical category, and the Symmetry/Antisymmetry/Encastre type; then press Continue.
2. Select the plane corresponding to X axis. Name it as ‘X’. Select the XSYMM option, and press OK.
3. Repeat the similar process for the other two plane surfaces.
4. For the displacement mapping on the curved surface, the boundary condition should be apply on specific set of nodes, otherwise errors of overlapping boundary conditions will appear. So we first make the meshes then come back for the rest boundary conditions.
Let’s do the mesh generation. Select the Mesh module.
1. Select ‘Seed Part Instance’. Change the ‘Approximate global size’ to 0.001 and click Apply, OK.
2. Select ‘Assign Element Type’ and select the 1/8 sphere. Check the box of ‘Hybrid formulation’ and leave the others as their default values. You should see you are using ‘C3D8RH’ elements.
3. Click on ‘Mesh Part Instance’ to generate the meshes.
Create the sets of nodes for applying boundary conditions. You can find all the current sets in the left model database tree inside Assembly>Sets fold.
1. Right click ‘Sets’ and select ‘Create…’. In the popup window, name it as ‘SurfAll’ and choose Type ‘Node’. In the bottom menu, ‘select the nodes for the set’ ‘by angle’. Click on the curved surface and press done.
2. Create a set named ‘EdgeX’ containing the nodes on the edge of the curved surface corresponding to X axis. In the bottom menu, ‘select the nodes for the set’ ‘by feature edge’. Create sets ‘EdgeY’ and ‘EdgeZ’ similarly.
3. Now we are going to create the desired sets of surface nodes by boolean operation. Use ‘Ctrl’ key to select both SurfAll and EdgeX, right click and choose ‘Boolean…’ in the menu. Name the new set ‘SurfX’ and select ‘Difference’ as the operation. Make sure that the ‘First set’ is SurfAll. Repeat the similar process to create ‘SurfY’ and ‘SurfZ’.
4. Now the left model database tree should look like .
Next, we come back to ‘Load’ module to finish the rest of the boundary conditions.
1. Create a ‘Displacement/Rotation’ boundary condition named ‘dx’ at Step-1. Select ‘Set’ in the right bottom menu and choose SurfX.
2. In the popup window, click on ‘f(x)’ to create an Analytical Fieid. Name it as ‘X’ and enter just ‘X’ for the expression.
3. Select ‘(A)X’ for ‘Distribution’. Check on box ‘U1’ and input ‘-7.72e-3’ for the magnitude of the displacement.
4. Create similar boundary condition ‘dy’ and ‘dz’ on ‘SurfY’ and ‘SurfZ’, respectively. Be sure to create Analytical Field ‘Y’ and ‘Z’, and define the displacement magnitude U2 = ‘-5.27e-3’ and U3 = ‘-6.34e-3’, respectively.
5. After all the boundary conditions are set up, you should see .
Great! This is the final step for the modeling. You will need to set up and submit an analysis. Select the Job module to do this
1. Select ‘Create Job’.
2. Name the job ‘Ellipsoid’. You can accept the defaults for all other options, and press OK.
3. To run the analysis, select ‘Submit’. If Abaqus detects any problems in defining the analysis, it will throw errors and warnings.
4. You can view the progress of the analysis, along with warning messages, by selecting ‘Monitor’. You will see two or three warnings, which are harmless. As the analysis runs, information about each step will be displayed in the Monitor window.
Abaqus also creates a large number of files during an analysis. You can find them in the Abaqus working directory. The following files can be viewed using a text editor and may contain useful information (eg. error messages if an analysis fails). It’s worth checking each to see what they contain:
1. Ellipsoid.inp is an ASCII file that defines the finite element simulation. This is how Abaqus/CAE (which is just a GUI) communicates with the Abaqus finite element platform. We often edit this file and run Abaqus with it directly when we use Abaqus with user element or user material subroutines.
2. Ellipsoid.log summarizes the outcome of each phase of the analysis.
3. Ellipsoid.sta is updated during analysis to show its progress.
4. Ellipsoid.msg contains error messages.
5. Ellipsoid.dat contains both error messages and the output of an analysis. It is sometimes the only way to easily view results of an analysis that has user elements.
Once the job is completed, you can view the results. To do so, start by selecting the Visualization module.
1. You will need to load the ‘output database’ by using File>Open… then navigate to the Abaqus working directory (if needed), and open the file called Ellipsoid.odb.
2. You can now explore the results of the simulation. For example, to plot von Mises stress contours on the deformed mesh, select .
3. You can view an animation of the deformation by selecting Animate > Time History. You can change the behavior of the animation by selecting the Options > Animation menu.
4. If you would like to plot contours of variables other than the von Mises stress, go to Result>Field Output. The Field Output menu will allow you to select different variables. If you don’t see the variable you want to plot that usually means Abaqus did not save it to the odb. To get it, you will need to go back to the Step menu, and use the Output> menu to add the variable you are interested in. The analysis will need to be re-run.
5. You can change the way the contour plots look by using the Options>Common menu, or Options>Contour.
6. Some additional features of the viewport can be controlled using the Viewport>Viewport Annotation Options.
7. You often want to change the background of the viewport to save plots for reports – you can do this using the View>Graphics Options menu.
8. The visualization module has many other features; if you have time, the best way to learn them is just to explore all the various options and see what happens.

Reference: This tutorial is mainly based on Prof. Allan Bower’s lecture notes for ENGN2340 Fall 2015. You can find more about Python scripting in Abaqus in this note.