Spring2024
\[\newcommand{\u}[1]{\boldsymbol{\mathsf{#1}}} \renewcommand{\b}[1]{\boldsymbol{#1}} \newcommand{\t}[1]{\textsf{#1}} \newcommand{\m}[1]{\mathbb{#1}} \def\RR{\bf R} \def\bold#1{\bf #1} \def\mbf#1{\mathbf #1} \def\uv#1{\hat{\usf {#1}}} \def\dl#1{\underline{\underline{#1}}} \newcommand{\usf}[1]{\boldsymbol{\mathsf{#1}}} \def\bs#1{\usf #1}\]Degree of freedom
Degrees of Freedom The minimum number of real numbers we need to specify in oder to completely know the configuration of the mechanical system.
Remark : The DoF are also called co-ordinates.
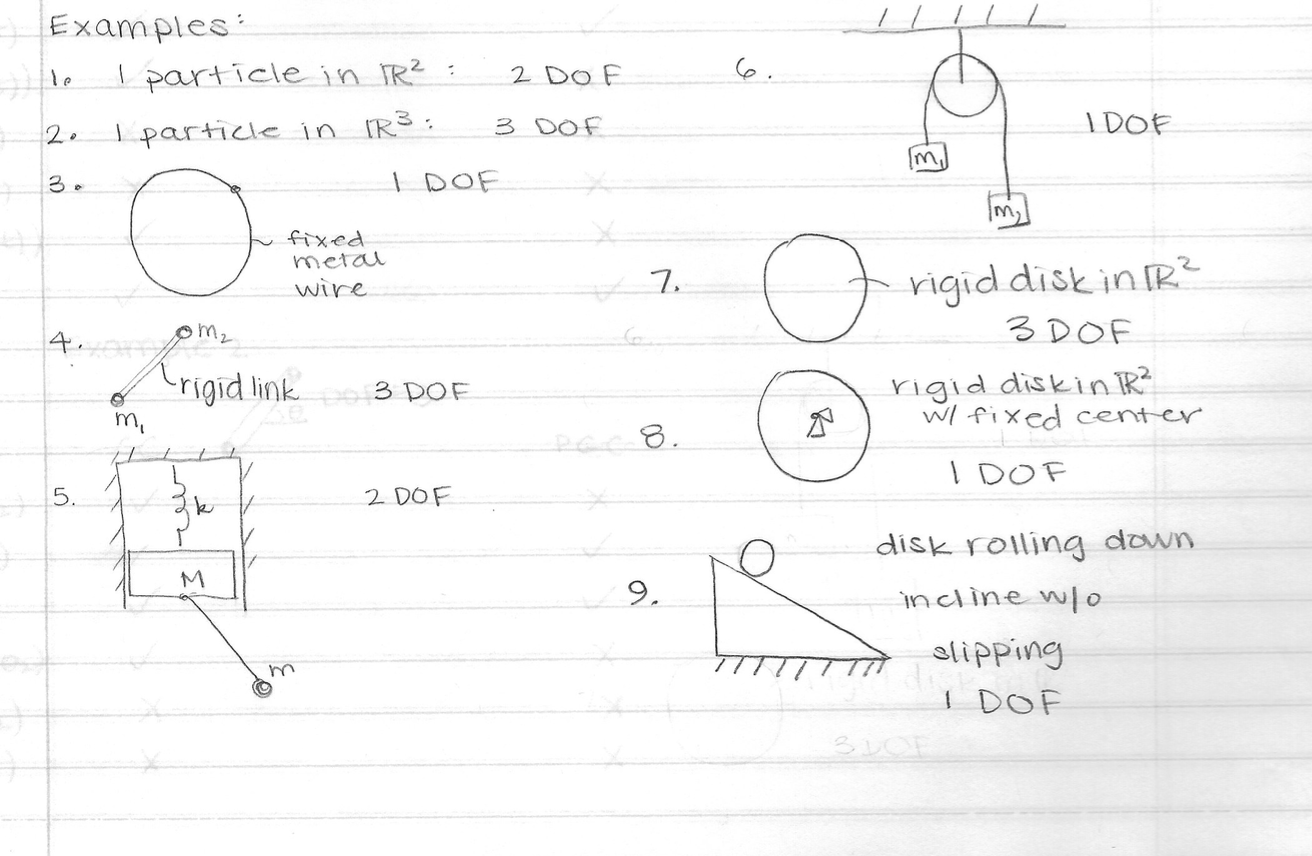
- 1 particle in $\mathbb{R}^2$ (2 DoF)
- 1 particle in $\mathbb{R}^3$ (3 DoF)
- A particle in a hoop. The hoop lies in $\mathbb{R}^2$ (1 DoF)
- A particle in a hoop. The hoop lies in in $\mathbb{R}^3$. (1 DoF)
- Two masses connected by a rigid link. The center point is fixed. The whole assembly lies in 2D (1 DoF).
- Now the center point is free (3 Dof)
- The whole assembly lies in 3D, with the center point fixed. (3 DoF)
- The whole assembly lies in 3D, with the center point free to two move. (6 DoF).
- A mass $M$ is constrained to lie in a slot. It is connected by a spring to the slot. There is a mass $m$ connected by a rigid link to the $M$ through a hinge (2D) joint. (2 DoF)
- A pulley with two hanging masses (1 DoF)
- A rigid disk in 2D (3 DoF)
- A rigid disk in 2D with center fixed. 1Dof
- A disk rolling down the wedge, the wedge is fixed. (1 DoF)
Generalized co-ordinates: A set of generalized co-ordinates is a set of real numbers (parameters) that when provided enable us to reconstruct the configuration of the mechanical system, and all configurations can be described this way. The generalized co-ordinates are customerily written as $(q_1,q_2, \ldots, q_n)$, or simply as $q_j$
Proper set of generalized